Курсовая работа: Разработка сменного модуля для изучения соединения типа "Звезда"
Для определения входных сопротивлений Z1вх и Z2вх можно воспользоваться любым из типов уравнений, однако наиболее простые выражения получаются, если соответственно выбрать уравнения типов А и В:
![]() ;
;
![]() ;
;
В частном случае при отключенном или закороченном приемнике входные сопротивления характеризуют только сам четырехполюсник, а следовательно, зависят только от его коэффициентов.

Рис. 1.5
При питании со стороны первичных выводов и коротком замыкании вторичных (рис. 1.5), т.е. при Z2н = 0, входное сопротивление
![]()
При холостом ходе на вторичных выводах, т.е. при ![]() , входное сопротивление
, входное сопротивление
![]()
Сопротивления короткого замыкания и холостого хода четырехполюсника однозначно определяются его коэффициентами.
Режим работы четырехполюсника, как и любой электрической цепи, можно характеризовать передаточными функциями при заданном сопротивлении приемника, т.е. в отличие от коэффициентов четырехполюсника передаточная функция зависит не только от структуры и параметров составляющих четырехполюсник элементов, но и от параметров приемника. Если, например, источник питания подключен к первичным выводам (см. рис. 1.3), то при сопротивлении нагрузки Z 2н можно составить различные передаточные функции, например ![]() и т.д.
и т.д.
1.3 Коэффициенты четырехполюсников
Коэффициенты уравнений постоянны и определяются только структурой четырехполюсника и параметрами составляющих его элементов, а не параметрами источника питания и приемника. С точки зрения режима на первичных и вторичных выводах четырёхполюсники, имеющие одинаковые значения коэффициентов, неотличимы, т.е. эквивалентны, хотя их внутренняя структура может быть совсем различной.
Таким образом, можно утверждать, что четырёхполюсник задан, если известны его коэффициенты.
Уравнения четырёхполюсника показывают, что проходной активный неавтономный или пассивный четырёхполюсник задаётся четырьмя коэффициентами любого из типов уравнений. Поэтому матрица коэффициентов одного из типов уравнений может быть выражена через матрицу коэффициентов любого другого типа уравнений.
Коэффициенты уравнений четырёхполюсника называют ещё его первичными параметрами. Каждый из первичных параметров имеет простой физический смысл. Например, по ![]() при
при ![]() (в режиме холостого хода на вторичных выводах), т.е.
(в режиме холостого хода на вторичных выводах), т.е. ![]() – входное сопротивление, измеренное на первичных выводах при разомкнутых вторичных. Если известна схема четырёхполюсника и значения составляющих его элементов, то любой из коэффициентов может быть определён расчетом.
– входное сопротивление, измеренное на первичных выводах при разомкнутых вторичных. Если известна схема четырёхполюсника и значения составляющих его элементов, то любой из коэффициентов может быть определён расчетом.
Симметричный четырехполюсник. Четырехполюсник, у которого при взаимной замене первичных выводов и вторичных выводов режимы источника питания и приемника не изменяются, называется симметричным . У такого активного неавтономного четырехполюсника не четыре, а три независимых коэффициента, а у пассивного два. Например, как было показано выше, при питании четырехполюсника со стороны первичных выводов и разомкнутых вторичных Z1х =Z11 . При питании со стороны вторичных выводов и разомкнутых первичных у симметричного четырехполюсника должно быть такое же входное сопротивление Z2х =Z1х. Из уравнений ![]() или
или ![]() при I1 =0 получаем Z22 =U2 /I2 =Z2х , и, следовательно,
при I1 =0 получаем Z22 =U2 /I2 =Z2х , и, следовательно, ![]() .
.
Такие же рассуждения приводят к равенствам
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Если два Г-образных четырехполюсника соединить соответственно друг с другом выводами 1 и 1', то получится симметричный Т-образный четырехполюсник.
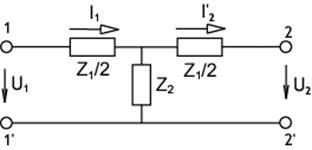
Рис. 1.6
Найдем коэффициенты уравнений типа А симметричного Т-образного четырехполюсника (рис. 1.6).
При холостом ходе на вторичных выводах (I'2 =0) из рис. 1.6 следует, что
![]() ;
; ![]() или
или ![]() . Сравнив эти выражения с уравнениями при
. Сравнив эти выражения с уравнениями при ![]() , определим
, определим
![]() ;
; ![]() .
.
При коротком замыкании вторичных выводов (![]() ) из рис. 1.6 следует, что
) из рис. 1.6 следует, что ![]() или
или ![]() ;
;
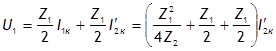 .
.
Сравнив эти выражения с уравнениями при U2 =0, найдем