Курсовая работа: Реализация класса для работы с комплексными числами

4. деление двух комплексных чисел;

5. нахождение n-ой степени комплексного числа;

6. вычисления корня n-ой степени комплексного числа;

7. перевод чисел из арифметической формы в тригонометрическую и в показательную;

Глава 2. ПРОЕКТИРОВАНИЕ ПРОГРАММНОГО МОДУЛЯ

2.1 Входные данные

В данной программе в качестве входных данных пользователю

необходимо ввести два комплексных числа, а также значение степени выполнения функции возведения в степень, степень для вычисления корня и номер корня комплексного числа. Ввод данных осуществляется с помощью клавиатуры.

2.2 Выходные данные

Выходные данные пользователь получает после введения всех входных данных и нажатия клавиши <Enter>.

Выходными данными являются комплексные числа в арифметической и (или) тригонометрической форме, полученные в результате выполнения операций над входными данными.

2.3 Описание данных, используемых при решении задачи

Комплексным числом называется выражение вида a + ib, где a и b – любые действительные числа, i – специальное число, которое называется мнимой единицей. Для таких выражений понятия равенства и операции сложения и умножения вводятся следующим образом:

1. два комплексных числа a + ib и c + id называются равными тогда и только тогда, когда a = b и c = d;

2. суммой двух комплексных чисел a + ib и c + id называется комплексное число a + c + i(b + d);

3. произведением двух комплексных чисел a + ib и c + id называется комплексное число ac – bd + i(ad + bc).

Комплексные числа часто обозначают одной буквой, например, z = a + ib. Действительное число a называется действительной частью комплексного числа z, действительная часть обозначается a = Re z. Действительное число b называется мнимой частью комплексного числа z, мнимая часть обозначается b = Im z.

Модулем комплексного числа называется длина вектора, соответствующего этому числу:

Модуль комплексного числа z обычно обозначается или r. Указанная в определении формула легко выводится при помощи теоремы Пифагора (см. рис. 1).

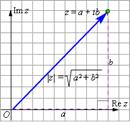
Рисунок1

Если то то есть для действительного числа модуль совпадает с абсолютной величиной. Ясно, что для всех При этом тогда и только тогда, когда

Арифметические операции над комплексными числами были определены в предыдущем пункте. Эти операции обладают следующими свойствами:

1. коммутативность сложения: z1 + z2 = z2 + z1 для любых .

2. ассоциативность сложения: (z1 + z2) + z3 = z1 + (z2 + z3) для любых .

3. существует такое число z = 0, которое обладает свойством z + 0 = z для любого z.

4. для любых двух чисел z1 и z2 существует такое число z, что z1 + z = z2. Такое число z называется разностью двух комплексных чисел и обозначается z = z2 – z1.

5. коммутативность умножения: z1z2 = z2z1 для любых .

6. ассоциативность умножения: (z1z2)z3 = z1(z2z3)

для любых .

7. дистрибутивность сложения относительно умножения: z1(z2 + z3) = z1z2 + z1z3 для любых.

8. для любого комплексного числа z:z · 1 = z.