Курсовая работа: Реализация класса для работы с комплексными числами

Деление на 0 невозможно.

Все указанные свойства доказываются с помощью определения операций сложения и умножения.

Если число z = a + bi, то число называется комплексно сопряжённым с числом z.

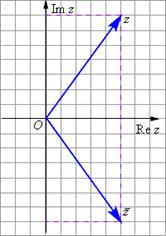
Рисунок2.

Пусть и φ = arg z. Тогда по определению аргумента имеем:

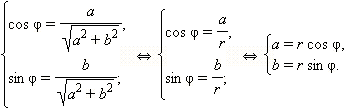
Отсюда получается

z = a + bi = r(cos φ + i sin φ).

Такая форма называется тригонометрической формой записи комплексного числа. Как видно, для того, чтобы перейти от алгебраической формы записи комплексного числа к тригонометрической форме, нужно найти его модуль и один из аргументов.

Арифметические действия над комплексными числами, записанными в тригонометрической форме, производятся следующим образом. Пусть z1 = r1(cos φ1 + i sin φ1) и z2 = r2(cos φ2 + i sin φ2). Имеем:

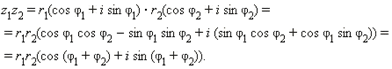
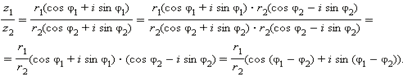
Первая формула Муавра:

Вторая формула Муавра:

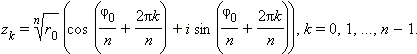
2.4 Описание схемы программы

	Вычисление f2

Глава 3 РЕАЛИЗАЦИЯ ПРОГРАММНОГО МОДУЛЯ

3.1 Описание используемых типов данных

В программе используются следующие типы данных:

1) Double – тип данных с плавающей точкой двойной точности. Диапазон значений от 1,7Е-308 до 1,7Е+308. Длина типа double вне зависимости от используемого компилятора всегда больше или равна длине типа float и короче или равна длине типа long double.

2) Int – предназначен для хранения целых чисел, входящих в диапазон от -2147489648 до +2147483647, имеет размер 32-разрядное целое число со знаком. Над переменными типа int могут выполняться следующие операции: сложение, вычитание, умножение, деление, целочисленное деление, деление с остатком.

3.2 Проектирование интерфейса

Данная программа разрабатывалась с помощью среды программирования Microsoft Visual Studio 2005. Программа является консольным приложением. Интерфейс программы во время выполнения:

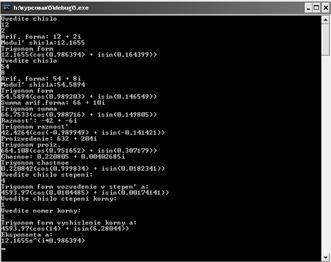
3.3 Написание кода для ввода и вывода исходных данных

Код для ввода и вывода данных:

void Complex::ShowComplex(){

cout << "Vvedite chislo" <<endl;

cin >> re;

cin >> im;

cout << "Arif. forma: " << re << " + " << im << "i" << endl;

double z=sqrt(re*re+im*im);