Курсовая работа: Реальные газы

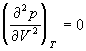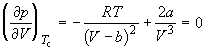По мере повышения температуры все три корня сближаются, и при критической температуре Tc все три корня становятся равными. В критической точке изотерма Ван-дер-Ваальса имеет точку перегиба с горизонтальной касательной , то есть и .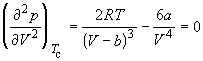

Совместное решение этих уравнений дает вывод критических параметров. Соответственно, согласно уравнению Ван-дер-Ваальса, критический фактор сжимаемости Z для всех газов должен быть равен:

Принципиальное значение уравнения Ван-дер-Ваальса определяется следующими обстоятельствами:

1) уравнение было получено из модельных представлений о свойствах реальных газов и жидкостей, а не явилось результатом эмпирического подбора функции f(p,V,T), описывающей свойства реальных газов;

2) уравнение долго рассматривалось как некоторый общий вид уравнения состояния реальных газов, на основе которого было построено много других уравнений состояния (см. ниже);

3) с помощью уравнения Ван-дер-Ваальса впервые удалось описать явление перехода газа в жидкость и проанализировать критические явления. В этом отношении уравнение Ван-дер-Ваальса имеет преимущество даже перед более точными уравнениями в вириальной форме (см. 1.1, 1.2).

Причиной недостаточной точности уравнения Ван-дер-Ваальс считал ассоциацию молекул в газовой фазе, которую не удается описать, учитывая зависимость параметров a и b от объема и температуры, без использования дополнительных постоянных. После 1873 г. сам Ван-дер-Ваальс предложил еще шесть вариантов своего уравнения, последнее из которых относится к 1911 г. и содержит пять эмпирических постоянных. Две модификации уравнения предложил Клаузиус, и обе они связаны с усложнением вида постоянной b. Больцман получил три уравнения этого типа, изменяя выражения для постоянной a. Всего известно более сотни подобных уравнений, отличающихся числом эмпирических постоянных, степенью точности и областью применимости. Выяснилось, что ни одно из уравнений состояния, содержащих менее 5 индивидуальных постоянных, не оказалось достаточно точным для описания реальных газов в широком диапазоне p, V, T, и все эти уравнения оказались непригодными в области конденсации газов. Из простых уравнений с двумя индивидуальными параметрами неплохие результаты дают уравнения Дитеричи и Бертло.

Вириальное уравнение состояния.

Поведение реального газа можно описать с высокой точностью с помощью вириального уравнения (или уравнения с вириальными коэффициентами). Идея состоит в отказе от минимального числа параметров и использовании бесконечных рядов - разложений по степеням 1/V:

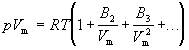
Коэффициенты B2, B3, ... (которые зависят от температуры и природы рассматриваемого газа, но не зависят от плотности и давления) называются соответственно вторым, третьим, ...вириальными коэффициентами. Первый вириальный коэффициент равен 1. Второй вириальный коэффициент обычно более важен, чем последующие, поскольку для большинства случаев B2 /Vm >> B3 /V2m >>... .

Уравнение состояния в виде бесконечного ряда было предложено Тиссеном в 1885 г. Однако основное развитие вириальное уравнение получило в 1901 г. в работе Камерлинг-Оннеса, который рассмотрел несколько вариантов этого уравнения и предложил называть его коэффициенты вириальными.

Если подходить в вириальному уравнению только как к эмпирическому уравнению состояния, то оно имеет ряд недостатков. Например, как показывают экспериментальные данные, сходимость ряда не очень хорошая, особенно в области высокой плотности. Кроме того, при высоких плотностях для удовлетворительного описания экспериментальных данных необходимо использовать большое число членов ряда, а для этого нужно экспериментально определять большое число вириальных коэффициентов. Более того, часто тот же набор экспериментальных данных можно более точно описать с помощью других эмпирических уравнений с меньшим числом параметров. Однако исключительная важность вириального уравнения состояния заключается в том, что это единственное из известных уравнений состояния, имеющее строгую теоретическую основу. Как будет показано в главе 2, каждый вириальный коэффициент можно выразить через силы межмолекулярного взаимодействия. Так, второй вириальный коэффициент отражает парные взаимодействия, третий – тройные и т.д. Таким образом, вириальное уравнение состояния позволяет объяснить свойства газа с позиции межмолекулярных взаимодействий.

Для некоторых целей вириальное уравнение удобнее записать в виде разложения по степеням p: pVm = RT (1 + B2'p + B3'p2 + ...)

Таким образом, вириальное уравнение является примером того, когда простое выражение (в данном случае pVm = RT) представляет собой только первый член ряда разложения по степеням переменной (в данном случае p или Vm).

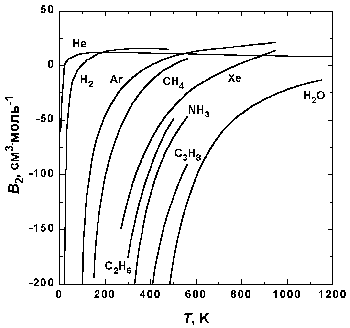
Рис.1.5. Зависимость второго вириального коэффициента некоторых газов от температуры.

На рис. 1.5 представлена зависимость второго вириального коэффициента от температуры для некоторых газов. При низких температурах B2 < 0, с ростом температуры его значение проходит через ноль, затем становится положительным, достигает максимума и далее очень медленно убывает. При высоких температурах B2 и все последующие вириальные коэффициенты стремятся к нулю. Температура, при которой B2 = 0, называется температурой Бойля TB.

Закон соответственных состояний.

Поскольку критические константы являются характеристическими свойствами газов, их можно использовать для создания соответствующей относительной шкалы, введя безразмерные приведенные переменные: приведенное давлениеpr(π), приведенный объем Vr(φ) и приведенную температуру Tr(τ):

;;.

Соответственными называются состояния разных веществ, имеющие одинаковые значения приведенных переменных. Согласно закону соответственных состояний, если для рассматриваемых веществ значения двух приведенных переменных одинаковы, должны совпадать и значения третьей приведенной переменной. Таким образом, уравнения состояния различных веществ, записанные в приведенных переменных, должны совпадать. Это утверждение эквивалентно постулату о существовании общего универсального приведенного уравнения состояния: F(pr, Vr, Tr) = 0

Поскольку это приведенное уравнение не содержит в явном виде индивидуальных постоянных, оно должно быть применимо к любому веществу. Закон соответственных состояний является общим утверждением, не связанным с конкретным видом уравнения состояния. На практике закон соответственных состояний приближенно выполняется для однотипных веществ, что позволяет, например, использовать для реальных газов обобщенные диаграммы сжимаемости.

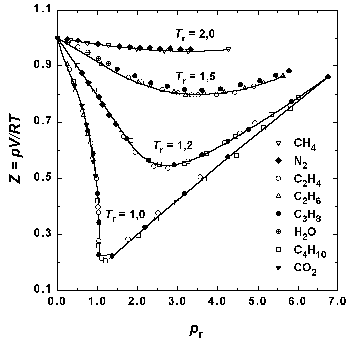
Рис.1.6. Зависимость фактора сжимаемости некоторых газов от приведенного давления при разных приведенных температурах.

Можно показать, что любое уравнение состояния, содержащее три параметра, можно представить в приведенной форме. Для тех из них, которые содержат три параметра, представлена также и приведенная форма. Отсутствие универсального уравнения F(pr, Vr, Tr) = 0 говорит не о неверности закона о соответственных состояниях, а о недостаточности двух индивидуальных постоянных и R в уравнении состояния.

В настоящее время понятно, почему в уравнениях состояния реальных газов двух индивидуальных параметров в общем случае не хватает, но в первом приближении этого достаточно. Причиной всех отклонений от уравнения состояния идеального газа являются межмолекулярные взаимодействия в газах.

Статистический расчет показывает, что наличие индивидуальных постоянных в уравнении межмолекулярного взаимодействия всегда приводит к появлению индивидуальных постоянных и в уравнении состояния газов. Поэтому в области значений p, V и T, для которых в реальных газах вклад межмолекулярных взаимодействий достаточно велик, в уравнениях состояния появляются индивидуальные постоянные, зависящие от параметров уравнении межмолекулярного взаимодействия. Поэтому в приближенных уравнениях состояния часто оказывается достаточно использовать две индивидуальные постоянные. Если же требуется описать поведение газа с более высокой точностью, необходимо использовать уравнения с бу льшим числом постоянных. Так, например, уравнение Битти – Бриджмена содержит пять постоянных кроме R и считается одним из лучших эмпирических уравнений состояния. В течение некоторого времени оно применялось при составлении справочных таблиц реальных газов. В настоящее время для возможно более точного описания свойств газов используют эмпирическое уравнение Бенедикта – Вебба – Рубина:

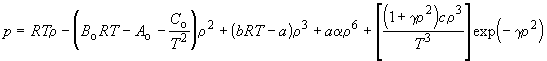
Модельные представления о реальных газах.