Если A - матрица с доминирующей диагональю, т.е. 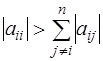, то метод Зейделя сходится при любом начальном приближении x ^{(0 )} .

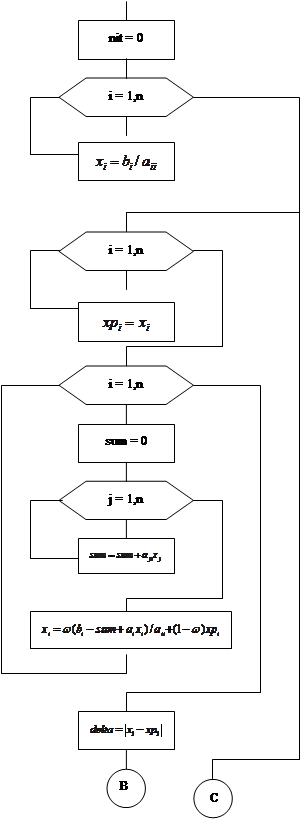
Метод Зейделя сходится примерно так же, как геометрическая прогрессия со знаменателем || G | | . Если норма матрицы G близка к 1, то скорость сходимости очень медленная. Для ускорения сходимости используется метод релаксации . Суть его в том, что полученное по методу Зейделя очередное значение пересчитывается по формуле:

Здесь 0<w£2 – параметр релаксации. Если w<1 - нижняя релаксация , если w>1 – верхняя релаксация . Параметр w подбирают так, чтобы сходимость метода достигалась за минимальное число итераций.

Метод Зейделя является одношаговым итерационным методам , когда для нахождения x ^{( k +1)} требуется помнить только одну предыдущую итерацию x ^{( k )} .

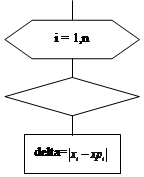
Погрешность итерации вычисляется по формуле:

n - порядок матрицы A.

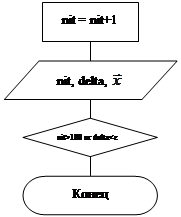
Если d меньше заданной точности e, то итерационный процесс прекращают.

Элементы главной диагонали называются главными. Заметим, что если в ходе расчётов по данному алгоритму на главной диагонали окажется нулевой элемент, то произойдет сбой программы. Для того, чтобы избежать этого, следует перестановку строк таким образом, чтобы на главной диагонали находились максимальные элементы строк. Т. е., если в k-й строке максимальным является i-й элемент, необходимо поменять местами k-ю и i-ю строки, и поменять местами соответствующие элементы вектора b. Такой выбор главного элемента необходим для сходимости итерационного процесса.

Приведём блок-схему реализации данного метода:

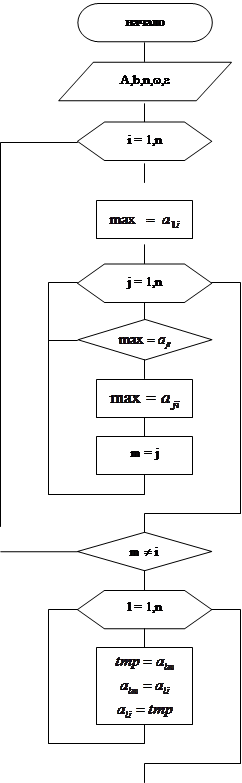
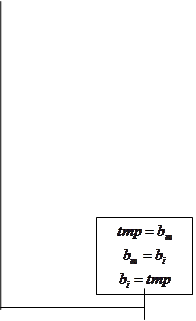3. Анализ результатов.

Скорость сходимости итерационного процесса зависит от заданной матрицы коэффициентов. В зависимости от вида исходных данных( матрицы коэффициентов и матрицы b) программа подбирает оптимальный параметр релаксации w(при котором решение достигается за минимальное число итераций).

Для достижения наивысшей скорости сходимости итерационного процесса для уравнения, заданного на рис.3 программой был выбран параметр релаксации w=1,26. Таким образом, была применена верхняя релаксация. Заданная точность e=0,0001 была достигнута за 40 итераций.

График зависимости количества итераций от параметра релаксации приведен на рис 1.

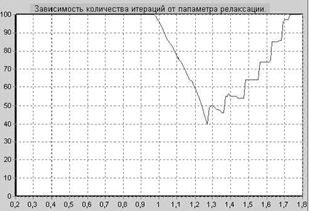Рис. 1

Для достижения наивысшей скорости сходимости итерационного процесса для уравнения, заданного на рис.4 программой был выбран параметр релаксации w=0,98. Таким образом, была применена нижняя релаксация. Заданная точность e=0,0001 была достигнута за 17 итераций. График зависимости количества итераций от параметра релаксации приведен на рис 2.

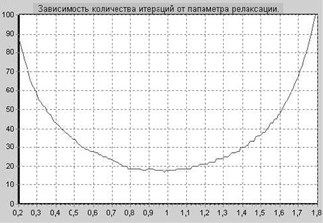Рис. 2

Правильность решения СЛАУ была проверена с помощью программного пакета Mathcad 2000 professional. Отметим, что программа даёт правильное решение СЛАУ почти во всех случаях, когда каждый элемент главной диагонали является максимальным в своей строке.

Вывод

Программа, разработанная в данной курсовой работе, реализует метод Зейделя для решения СЛАУ 6-го порядка. Она даёт гарантированно правильное решение системы линейных уравнений, если каждый элемент главной диагонали матрицы коэффициентов является единственным максимальным в своей строке, ненулевым, либо справедливы условия: максимальный элемент строки является единственным максимальным в своём столбце, ненулевым, а ни один из остальных элементов столбца не является максимальным в своей строке, все элементы каждой строки кроме максимального одинаковы.

При исходных данных:

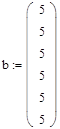
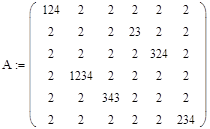
была достигнута точность 0,0001 в решении:

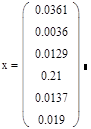?? 2 ???????? ??? ????????? ?????????? w=0,97.

Программа строит график зависимости количества итераций от параметра релаксации для данной СЛАУ, находит параметр релаксации w, при котором решение достигается за минимальное количество итераций и, разумеется, само решение. Программа проста в эксплуатации и нетребовательна к ресурсам. Реализованная в современной среде разработки Delphi 5.0, она без труда может быть доработана или исправлена.

Недостатки программы: 1) применима не для всех систем линейных уравнений; 2)оптимальный параметр релаксации w вычисляется методом подбора, и, поэтому, количество итераций, требуемое для его отыскания достаточно велико(около 18000), однако, для современных ПК, это не является затруднением.

Список использованной литературы

1. Волков Е.А. Численные методы. ¾ М.: Наука, 1987. ¾ 254 с.

2. Калиткин Н.Н. Численные методы. ¾ М.: Наука, 1978. ¾ 512 с.

3. Мудров А.Е. Численные методы для ПЭВМ на языках БЕЙСИК, ФОРТРАН и ПАСКАЛЬ. ¾ Томск, МП "Раско", 1992. ¾270 с.

4. Самарский А.А., Гулин А.В. Численные методы. ¾ М.: Наука, 1989. ¾432с.

5. Кэнту М. Delphi 4 для профессионалов ¾ СПб: «Питер», 1999 ¾1200с.

6. Delphi 5.0 help.

Приложение(распечатка программы, результатов)

Распечатка программы: