Курсовая работа: Решение задачи с помощью математической модели и средств MS Excel
Т. е. исследуем функцию вида:
![]()
Аналитическое исследование функции. Нахождение критических точек
Воспользуемся общей схемой исследования функции.
![]()
1. Найти область определения
Областью определения будут числа больше 0, т.к объем производства должен быть положительным, т.е. ![]() . Получим, что
. Получим, что
![]()
2. Найти (если это можно) точки пересечения графика с осями координат.
В нашем случае это невозможно, т.к ![]() , а решая квадратное уравнение вида
, а решая квадратное уравнение вида ![]() получаем мнимые корни (т.е. дискриминант меньше 0), следовательно, точек пересечения с осями координат нет.
получаем мнимые корни (т.е. дискриминант меньше 0), следовательно, точек пересечения с осями координат нет.
3. Найти интервалы знакопостоянства функции (промежутки, на которых ![]() или
или ![]() ). Координаты вершины параболы (3;
). Координаты вершины параболы (3;
6), значит, ![]() при
при ![]() , и
, и ![]() при
при ![]() .
.
4. Выяснить является ли функция четной, нечетной или общего вида.
Функция ![]() является функцией общего вида, т.к
является функцией общего вида, т.к
![]()
5. Найдите асимптоты графика функции.
Функция ![]() не имеет вертикальной, горизонтальной и наклонной асимптот.
не имеет вертикальной, горизонтальной и наклонной асимптот.
6. Найдите интервалы монотонности функции.
Для этого найдем первую производную от заданной функции:
![]()
![]()
Решим уравнение вида:
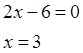
![]()
Получим, что в точке ![]() функция меняется, т.е. на промежутке
функция меняется, т.е. на промежутке ![]() функция монотонно убывает, а на
функция монотонно убывает, а на ![]() возрастает.
возрастает.
7. Найти экстремумы функции.
Из пункта 6 следует, что точка ![]() является критической, т. е экстремумом. Причем,
является критической, т. е экстремумом. Причем, ![]() - точка минимума.
- точка минимума.
Найдем значение функции в критической точке:
![]()
8. Найти точки перегиба функции.
Для этого найдем вторую производную от заданной функции: