Курсовая работа: Ряды и интеграл Фурье

( так как ).

Отдельно рассмотрим случай когда n=1:

.

Подставим найденные коэффициенты в получим:

и вообще

.

Найдем первые пять гармоник для найденного ряда:

1-ая гармоника ,

2-ая гармоника ,

3-ая гармоника ,

4-ая гармоника ,

5-ая гармоника ,

и общий график F(x), сумма выше перечисленных гармоник. и сами гармоники.

Запишем комплексную форму полученного ряда

Для рассматриваемого ряда получаем коэффициенты (см. теорию)

,

но при не существует, поэтому рассмотрим случай когда n =+1 :

(т.к. см. разложение выше)

и случай когда n =-1:

(т.к. )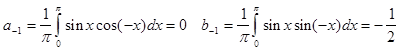

И вообще комплексная форма:

или

или