Курсовая работа: Розробка програми мовою програмування С++ по пошуку коренів нелінійних рівнянь
Відшукаємо значення ![]() з будь-якою точністю за таких допущень: функція
з будь-якою точністю за таких допущень: функція ![]() має на відрізку
має на відрізку ![]() неперервні похідні до другого порядку включно і, крім того, похідні
неперервні похідні до другого порядку включно і, крім того, похідні ![]() і
і ![]() зберігають знаки на цьому відрізку. Із цих умов випливає, що
зберігають знаки на цьому відрізку. Із цих умов випливає, що ![]() - монотонна функція на відрізку
- монотонна функція на відрізку ![]() , яка на кінцях має різні знаки, а також, що крива
, яка на кінцях має різні знаки, а також, що крива ![]() опукла або вгнута (рис. 1.1).
опукла або вгнута (рис. 1.1).
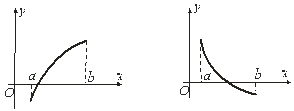
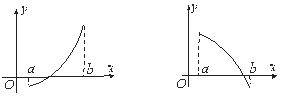
Рисунок 1.1 – Варіанти поведінки функції ![]()
Отже, розглянемо задачу знаходження коренів рівняння
![]() , (1)
, (1)
де ![]() - задана функція дійсного змінного.
- задана функція дійсного змінного.
Розв’язування даної задачі можна розкласти на декілька етапів:
а) дослідження розташування коренів (в загальному випадку на комплексній площині) та їх кратність;
б) відділення коренів, тобто виділення областей, що містять тільки один корінь;
в) обчислення кореня з заданою точністю за допомогою одного з ітераційних алгоритмів.
Далі розглядаються ітераційні процеси, що дають можливість побудувати числову послідовність xn , яка збігається до шуканого кореня ![]() рівняння (1).
рівняння (1).
Метод ділення проміжку навпіл (метод дихотомії)
Нехай ![]() і відомо, що рівняння (1) має єдиний корінь
і відомо, що рівняння (1) має єдиний корінь ![]() . Покладемо a0 =a, b0 =b, x0 =(a0 +b0 )/2. Якщо
. Покладемо a0 =a, b0 =b, x0 =(a0 +b0 )/2. Якщо ![]() , то
, то ![]() . Якщо
. Якщо ![]() , то покладемо
, то покладемо
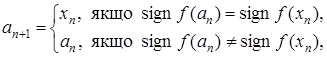 (2)
(2)
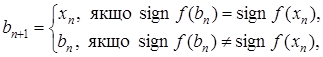 (3)
(3)
![]() (4)
(4)
і обчислимо ![]() . Якщо
. Якщо ![]() , то ітераційний процес зупинимо і будемо вважати, що
, то ітераційний процес зупинимо і будемо вважати, що ![]() . Якщо
. Якщо ![]() , то повторюємо розрахунки за формулами (2)-(4).
, то повторюємо розрахунки за формулами (2)-(4).
З формул (2), (3) видно, що ![]() і
і ![]() . Тому
. Тому ![]() , а отже шуканий корінь
, а отже шуканий корінь ![]() знаходиться на проміжку
знаходиться на проміжку ![]() . При цьому має місце оцінка збіжності
. При цьому має місце оцінка збіжності
![]() . (5)
. (5)
Звідси випливає, що кількість ітерацій. які необхідно провести для знаходження наближеного кореня рівняння (1) з заданою точністю e задовольняє співвідношенню
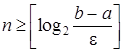 . (6)
. (6)
де [c] - ціла частина числа c.
Серед переваг даного методу слід відзначити простоту реалізації та надійність. Послідовність {xn } збігається до кореня ![]() для довільних неперервних функцій f(x). До недоліків можна віднести невисоку швидкість збіжності методу та неможливість безпосереднього узагальнення систем нелінійних рівнянь.
для довільних неперервних функцій f(x). До недоліків можна віднести невисоку швидкість збіжності методу та неможливість безпосереднього узагальнення систем нелінійних рівнянь.
Метод простої ітерації
Метод простої ітерації застосовується до розв’язування нелінійного рівняння виду
![]() . (7)
. (7)
Перейти від рівняння (1) до рівняння(7) можна багатьма способами, наприклад, вибравши
![]() , (8)
, (8)
де ![]() - довільна знакостала неперервна функція.
- довільна знакостала неперервна функція.
Вибравши нульове наближення x0 , наступні наближення знаходяться за формулою