Курсовая работа: Розробка програми мовою програмування С++ по пошуку коренів нелінійних рівнянь

Наведемо достатні умови збіжності методу простої ітерації.

Теорема 1. Нехай для вибраного початкового наближення x₀ на проміжку

(10)

функція j(x) задовольняє умові Ліпшиця

(11)

де 0<q<1, і виконується нерівність

. (12)

Тоді рівняння (7) має на проміжку S єдиний корінь , до якого збігається послідовність (9), причому швидкість збіжності визначається нерівністю

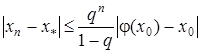. (13)

Зауваження: якщо функція j(x) має на проміжку S неперервну похідну , яка задовольняє умові

, (14)

то функція j(x) буде задовольняти умові (11) теореми 1.

З (13) можна отримати оцінку кількості ітерацій. які потрібно провести для знаходження розв’язку задачі (7) з наперед заданою точністю e:

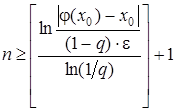. (15)

Наведемо ще одну оцінку. що характеризує збіжність методу простої ітерації:

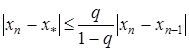. (16)

Метод релаксації

Для збіжності ітераційного процесу (9) суттєве значення має вибір функції j(x). Зокрема, якщо в (8) вибрати , то отримаємо метод релаксації.

, (17)

який збігається при

. (18)

Якщо в деякому околі кореня виконуються умови

, (19)

то метод релаксації збігаються при . Збіжність буде найкращою при

. (20)

При такому виборі t для похибки буде мати місце оцінка

, (21)

де .

Кількість ітерацій, які потрібно провести для знаходження розв’язку з точністю e визначається нерівністю

. (22)