Курсовая работа: Розвязок інтеграла методом Чебиша Гауса Сімпсона
Додаток А. Технічне завдання.
Додаток Б Структура дискети.
Анотація
В даній курсовій роботі розроблено комплекс програм для застосування точного рiвняння Ейлера-Бернулi для великих деформацiй бруса, а саме для обчислення значення еліптичного інтеграла за допомогою чисельних методів Сімпсона, Чебишева та Гауса. Описано алгоритм розв'язку поставленої задачі. Складено програму на мові Turbo C++.
Вступ
В наш час науково-технічний прогрес невідривно пов’язаний з бурхливим розвитком систем управління і автоматики. Автоматика – це галузь науки і техніки, яка охоплює теорію та принципи побудови систем управління процесами, що діють без безпосередньої участі людини. У відповідності до загальних принципів управління різними процесами, автоматичне управління здійснюється на основі інформації з використанням комплексу технічних засобів.
Автоматизація технологічних процесів на основі застосування автоматизованих станків, машин та механізмів, робототехнічних комплексів, сучасних засобів автоматики та обчислювальної техніки складає один з головних напрямків науково технічного прогресу в усіх галузях народного господарства. Вирішення задач автоматизації в наш час неможливе без застосування досягнень мікроелектроніки, яка забезпечує випуск елементної бази для пристроїв автоматики та систем управління в цілому.
1 Огляд та варіантний аналіз чисельних методів дослідження еліптичного інтегралу першого порядку
1.1 Основні поняття та визначення
Інтеграл є основним поняттям інтегрального числення.
Нехай f(x) – неперервна функція, а функція F(x) така, що її похідна дорівнює f(x), тобто F’(x)=f(x). Таку функцію F(x) називають інтегралом, або первісною функцією, відносно f(x). Разом з F(x) первісною відносно f(x) є і F(x)+С, де С – довільна константа. Вираз F(x)+С називається невизначеним інтегралом для f(x) і позначають 
.
Нехай функція f(x) неперервна на відрізку [a, b]. Розділимо [a, b] на частини точками a=x0 <x1 <x2 <…<xn =b і складемо так звану інтегральну суму
,
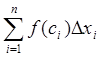де xi-1 <ci <xi , Dxi =xi -xi-1 . Визначеним інтегралом функції на відрізку [a, b] називається границя, до якої прямує інтегральна сума, коли найбільша різниця Dxi прямує до нуля; його позначають 
.
Застосування точного рiвняння Ейлера-Бернулi для великих деформацiй бруса призводить до еліптичних інтегралів. Еліптичний інтеграл першого порядку (роду) записується у вигляді:
,
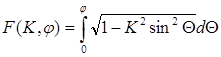де 0£К£1.
Чисельні методи – методи наближеного вирішення математичних задач, які зводяться до скінченого числа елементарних операцій над числами. Під елементарними операціями розуміють арифметичні та логічні дії, а також допоміжні операції (записи проміжних операцій, вибірки із таблиць тощо). Розробка нових числових методів і застосування їх на ЕОМ привели до виникнення обчислювальної математики.
1.2 Класифікація методів рішення поставленої задачі
 |
Рис. 1.1 Класифікація методів чисельного обчислення визначених інтегралів
Метод Сімпсона – частинний випадок метода Ньютона-Котеса при n=2. Цей метод досить точний навіть для многочленів третього степеня. Ця особливість методу пояснює його переважне застосування на ЕОМ.
Метод Чебишева – чисельний метод обчислення визначених інтегралів, який характеризується великою точністю обчислень для поліномів степеня n.
Метод Гауса - чисельний метод обчислення визначених інтегралів, який базується на інтерполяції поліномом Лагранжа, але абсциси вибираються із умови забезпечення мінімума похибки інтерполяції. Цей метод забезпечую підвищену точність.
1.3 Опис методів дослідження еліптичного інтегралу першого порядку на ЕОМ
Метод Сімпсона реалізується наступною формулою:
,
де h - крок інтегрування.
Похибка методу R~(h5 ).
Метод Чебишева реалізується застосуванням формули:
,
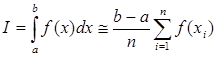де 
;
; 
; 
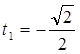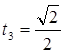, при n=3.
Метод Гауса реалізується за допомогою формули:
,
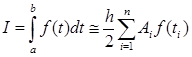де 
; ; 
; 
; 
; 
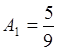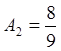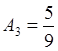, при n=3.