Курсовая работа: Розвязок інтеграла методом Чебиша Гауса Сімпсона
а) методом Сімпсона, б) методом Чебишева, в) методом Гауса
Як видно із рис. 4.1 табличні значення інтегралу, отримані різними методами: Сімпсона, Чебишева, Гауса відрізняються несуттєво, що свідчить про високу точність цих методів.
4.4 Тестова перевірка чисельних методів

а)
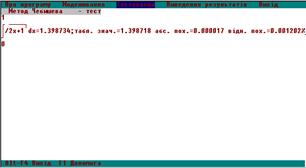
б)
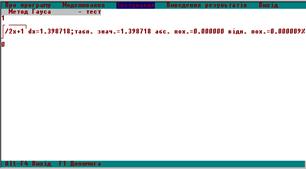
в)
Рис. 4.2. Тестова перевірка чисельних методів:
а) методом Сімпсона, б) методом Чебишева, в) методом Гауса
5 Оцінка похибок отриманих результатів
Оцінка похибок результатів дослідження проводилася шляхом порівняння табличних значень інтегралів (рис. 4.2), отриманих за допомогою розробленого програмного комплексу з тестовим прикладом. Результати цієї оцінки наведені в табл. 5.1.
Таблиця 5.1 - Оцінка похибок результатів дослідження
|
Метод |
Абсолютна похибка |
Відносна похибка, % |
|
Сімпсона |
0,000004 |
0,000256 |
|
Чебишева |
0,000017 |
0,001202 |
|
Гауса |
0,000000 |
0,000009 |
Відносна похибка розрахунків дуже мала, що є цілком прийнятним. Найбільш точний метод Гауса.
6 Оцінка ефективності комплексу програм для дослідження
Таблиця 6.1 - Оцінка ефективності комплексу програм для дослідження
|
Зміст |
Назва |
Розмір, байт |
К-во Просмотров: 563
Бесплатно скачать Курсовая работа: Розвязок інтеграла методом Чебиша Гауса Сімпсона
|