When all the tricks we've talked about so far are put together, scenes of tremendous realism can be created. And in recent games and films, computer-generated objects are combined with photographic backgrounds to further heighten the illusion. You can see the amazing results when you compare photographs and computer-generated scenes.

This is a photograph of a sidewalk near the How Stuff Works office. In one of the following images, a ball was placed on the sidewalk and photographed. In the other, an artist used a computer graphics program to create a ball.

Image A Image B

Can you tell which is the real ball? Look for the answer at the end of the article.

Making 3D Graphics Move

So far, we've been looking at the sorts of things that make any digital image seem more realistic, whether the image is a single "still" picture or part of an animated sequence. But during an animated sequence, programmers and designers will use even more tricks to give the appearance of "live action" rather than of computer-generated images.

How many frames per second ?

When you go to see a movie at the local theater, a sequence of images called frames runs in front of your eyes at a rate of 24 frames per second. Since your retina will retain an image for a bit longer than 1/24th of a second, most people's eyes will blend the frames into a single, continuous image of movement and action.

If you think of this from the other direction, it means that each frame of a motion picture is a photograph taken at an exposure of 1/24 of a second. That's much longer than the exposures taken for "stop action" photography, in which runners and other objects in motion seem frozen in flight. As a result, if you look at a single frame from a movie about racing, you see that some of the cars are "blurred" because they moved during the time that the camera shutter was open. This blurring of things that are moving fast is something that we're used to seeing, and it's part of what makes an image look real to us when we see it on a screen.

However, since digital 3D images are not photographs at all, no blurring occurs when an object moves during a frame. To make images look more realistic, blurring has to be explicitly added by programmers. Some designers feel that "overcoming" this lack of natural blurring requires more than 30 frames per second, and have pushed their games to display 60 frames per second. While this allows each individual image to be rendered in great detail, and movements to be shown in smaller increments, it dramatically increases the number of frames that must be rendered for a given sequence of action. As an example, think of a chase that lasts six and one-half minutes. A motion picture would require 24 (frames per second) x 60 (seconds) x 6.5 (minutes) or 9,360 frames for the chase. A digital 3D image at 60 frames per second would require 60 x 60 x 6.5, or 23,400 frames for the same length of time.

Creative Blurring

The blurring that programmers add to boost realism in a moving image is called "motion blur" or "spatial anti-aliasing." If you've ever turned on the "mouse trails" feature of Windows, you've used a very crude version of a portion of this technique. Copies of the moving object are left behind in its wake, with the copies growing ever less distinct and intense as the object moves farther away. The length of the trail of the object, how quickly the copies fade away and other details will vary depending on exactly how fast the object is supposed to be moving, how close to the viewer it is, and the extent to which it is the focus of attention. As you can see, there are a lot of decisions to be made and many details to be programmed in making an object appear to move realistically.

There are other parts of an image where the precise rendering of a computer must be sacrificed for the sake of realism. This applies both to still and moving images. Reflections are a good example. You've seen the images of chrome-surfaced cars and spaceships perfectly reflecting everything in the scene. While the chrome-covered images are tremendous demonstrations of ray-tracing, most of us don't live in chrome-plated worlds. Wooden furniture, marble floors and polished metal all reflect images, though not as perfectly as a smooth mirror. The reflections in these surfaces must be blurred -- with each surface receiving a different blur -- so that the surfaces surrounding the central players in a digital drama provide a realistic stage for the action.

Fluid Motion for Us Is Hard Work for the Computer

All the factors we've discussed so far add complexity to the process of putting a 3D image on the screen. It's harder to define and create the object in the first place, and it's harder to render it by generating all the pixels needed to display the image. The triangles and polygons of the wireframe, the texture of the surface, and the rays of light coming from various light sources and reflecting from multiple surfaces must all be calculated and assembled before the software begins to tell the computer how to paint the pixels on the screen. You might think that the hard work of computing would be over when the painting begins, but it's at the painting, or rendering, level that the numbers begin to add up.

Today, a screen resolution of 1024 x 768 defines the lowest point of "high-resolution." That means that there are 786,432 picture elements, or pixels, to be painted on the screen. If there are 32 bits of color available, multiplying by 32 shows that 25,165,824 bits have to be dealt with to make a single image. Moving at a rate of 60 frames per second demands that the computer handle 1,509,949,440 bits of information every second just to put the image onto the screen. And this is completely separate from the work the computer has to do to decide about the content, colors, shapes, lighting and everything else about the image so that the pixels put on the screen actually show the right image. When you think about all the processing that has to happen just to get the image painted, it's easy to understand why graphics display boards are moving more and more of the graphics processing away from the computer's central processing unit (CPU). The CPU needs all the help it can get.

Transforms and Processors: Work, Work, Work

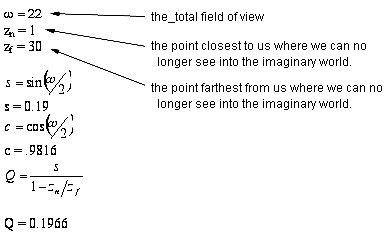
Looking at the number of information bits that go into the makeup of a screen only gives a partial picture of how much processing is involved. To get some inkling of the total processing load, we have to talk about a mathematical process called a transform. Transforms are used whenever we change the way we look at something. A picture of a car that moves toward us, for example, uses transforms to make the car appear larger as it moves. Another example of a transform is when the 3D world created by a computer program has to be "flattened" into 2-D for display on a screen. Let's look at the math involved with this transform -- one that's used in every frame of a 3D game -- to get an idea of what the computer is doing. We'll use some numbers that are made up but that give an idea of the staggering amount of mathematics involved in generating one screen. Don't worry about learning to do the math. That has become the computer's problem. This is all intended to give you some appreciation for the heavy-lifting your computer does when you run a game.

The first part of the process has several important variables:

X = 758 -- the height of the "world" we're looking at.

Y = 1024 -- the width of the world we're looking at

Z = 2 -- the depth (front to back) of the world we're looking at

Sx = height of our window into the world

Sy - width of our window into the world

Sz = a depth variable that determines which objects are visible in front of other, hidden objects

D = .75 -- the distance between our eye and the window in this imaginary world.

First, we calculate the size of the windows into the imaginary world.

Now that the window size has been calculated, a perspective transform is used to move a step closer to projecting the world onto a monitor screen. In this next step, we add some more variables.