Курсовая работа: Синтез та дослідження двійково-десяткового лічильника
1
Намалюємо діаграми Вейча для функційвходів тригерів:

Рисунок 2.3 – Діаграми Вейча для функцій
збудження тригерів. Синтез третій
Згідно діаграм Вейча запишемо значення функцій на D- та JK- входах тригерів для цього випадку.
K1= Т1
J1= Т1
K2= Т1
![]()
![]()
![]()
![]() J2= Т1 Т3 + Т1 Т4 =Т1+Т3+Т1+Т4
J2= Т1 Т3 + Т1 Т4 =Т1+Т3+Т1+Т4
![]()
![]()
![]()
![]()
![]()
![]() D3= Т1 Т2 Т4 + Т1 Т3=Т1+Т2+Т4+Т1+Т3
D3= Т1 Т2 Т4 + Т1 Т3=Т1+Т2+Т4+Т1+Т3
![]()
![]() K4= Т1 Т2 = Т1+Т2
K4= Т1 Т2 = Т1+Т2
![]()
![]() J4= Т1 Т2 =Т1+Т2
J4= Т1 Т2 =Т1+Т2
Складність апаратної реалізації цієї схеми за Квайном K=26 , що менше ніж у попередніх випадках, тому остання схема більш простіша і потребує меншої кількості апаратних витрат.
3 МАШИННЕ МОДЕЛЮВАННЯ
синхронний двійковий десятковий лічильник
Змоделювавши схему лічильника у середовищі «OrCAD» ми отримали схему, що зображена на рисунку 3.1.
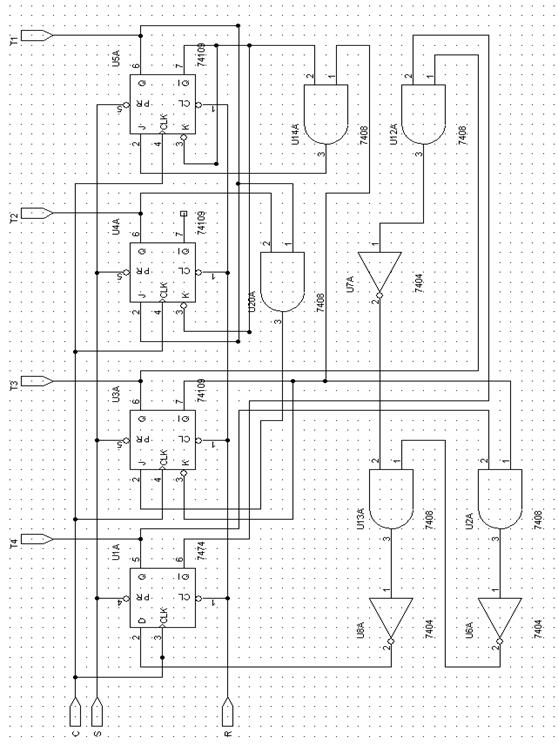
Рисунок 3.1 – Функціональна схема двійково-десяткового лічильника
Для правильної роботи лічильника, необхідно правильно задати вхідні сигнали, лише при цій умові вихідні сигнали будуть вірними. На R(анг. Reset – скинути)-вхід необхідно подати короткочасний «0» , на S(анг. Set – встановити) подаємо постійну одиницю, а на C(синхронний)-вхід подавати періодичний сигнал з періодом починаючи від 60нс. Дана схема нормально функціонує при 60нс, зображено на рисунку 3.2. Але це не мінімальний період. Тому, методом підбору, визначаємо, що мінімальний період має 53нс, роботу лічильника при мінімальному періоді зображено на рисунку 3.3.

Рисунок 3.2 – Часова діаграма роботи лічильника при періоді у 100нс
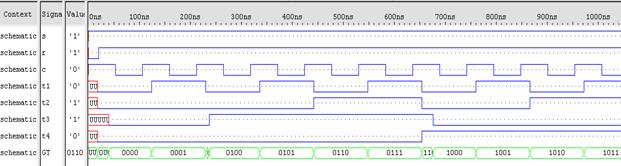
Рисунок 3.3 –Часова діаграма роботи лічильника при мінімальному періоді
Якщо період коливання на C-вході зменшити хоча б на одиницю, то лічильник перестане працювати коректно, відбуватиметься це тому, що цього періоду не буде достатньо щоб усі тригери лічильника прийняли правильний стан. У даному випадку найпершим відмовляє вихід Т3, причиню цього є те, що цей вихід обслуговується тригером D3, а D3 обслуговується найбільшою функцією, що є у схемі. Тобто ця функція має найбільшу затримку серед усіх реалізованих у схемі.
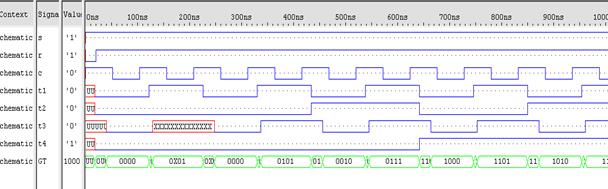
Рисунок 3.4 – Часова діаграма роботи лічильника при періоді,
меншому за мінімальний
Після визначення мінімального періоду потрібно визначити максимальну тактову частоту, вона обчислюється за формулою (3.1)
![]() (3.1)
(3.1)
Підставивши в формулу отримані значення визначимо максимальну тактову частоту (3.2)
![]() (3.2)
(3.2)
Також потрібно виміряти час реєстрації лічильника. Час реєстрації лічильника – це найбільший період часу протягом якого лічильник установиться у новий стан після дії активного (у даному випадку передній фронт на C-вході) значення сигналу. При дослідженні часової діаграми (рисунок 3.5) було виявлено, що час реєстрації дорівнює 18нс, але інколи між станами виникають короткочасні хибні стани, тому некоректно вважати, що час реєстрації складає саме 18нс.
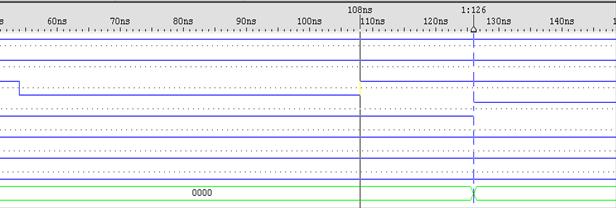
Рисунок 3.5 – Час реєстрації лічильника
ВИСНОВКИ
В даній курсовій роботі було синтезовано і промодельовано двійково-десятковий лічильник. Було проведено три синтези, для того щоб за Квайном визначити складність апаратної реалізації, і обрати найпростіший варіант. Найпростішим виявився останній варіант, зі складністю апаратної реалізації по Квайну K=26 . Лічильник було побудовано на елементах базису АБО,Ні.
Мінімізація функцій входів тригерів забезпечує мінімум апаратних витрат на реалізацію комбінаційної частини лічильника. З часової діаграми роботи двійково-десяткового лічильника видно, що лічильник проходить всі стани які відповідно кодують цифри від 0 до 9 (згідно таблиці функціонування), що й було необхідно.
Після побудови лічильника, його було досліджено, і виявлено найбільшу тактову частоту – 1МГц, і найменший період при якому схема працює - 53нс. Також було визначено час реєстрації лічильника – 18нс.
ЛІТЕРАТУРА
1. Пєтух А., Обідник Д. Схемотехніка ЕОМ. – Вінниця: ВДТУ 1999.
2. Пєтух А., Войтко В. Прикладна теорія цифрових автоматів. – Вінниця: ВДТУ, 2001.
3. Богданович М. И. и др. Цифровые интегральные микросхемы. – Минск: Беларусь, 1996. – 492 с.
4. Справочник по интегральным микросхемам / Б.В.Тарабрин и др.; Под ред. Б.В.Тарабрина. - М.: Энергия, 1985.
5. Самофалов К.Г. и др. Цифровые электронные вычислительные машины. Киев: Вища школа, 1983.