Курсовая работа: Схематическое моделирование при обучении решению задач на движение (младшие школьники)
— Если дано "общее" расстояние, то какую скорость мы найдём? (Найдём общую скорость.)
— Теперь, зная "общую скорость" и скорость первого автомобиля, что можно найти? (Скорость второго автомобиля.)
— Ответили мы на вопрос задачи? (Да.)
Весьма поучительно решение следующей четверки задач, исчерпывающих все возможные комбинации направлений движения двух тел относительно друг друга (рис.7). Вопрос для всех задач общий: через сколько секунд А и В окажутся рядом? Итак, дана задача: «Между двумя точками А и В имеются две дороги, длинная — 160 м и короткая — 80 м. Из этих точек движутся два велосипедиста со скоростями 5 и 3 м в секунду. Через сколько секунд они окажутся рядом? (Рассмотреть все возможные случаи.)»
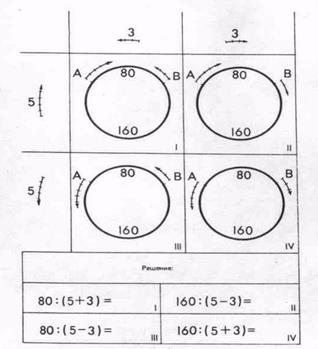
Решение задачи удобно изобразить в матрице с двумя входами.
Подобная четверка задач позволяет рассмотреть исчерпывающим образом математическую ситуацию, перебирая все возможные сочетания направлений движения двух тел. При таком оформлении четверки задач информация о направлении движения передается на нескольких кодах: по горизонтальному входу матрицы показаны скорости велосипедиста А, по вертикальному входу матрицы показаны скорости велосипедиста В. Эти же скорости изображены и на самих рисунках в матрице. По этой схеме удобно проводить обучающую беседу, позволяющую добыть дополнительную информацию об изучаемом.
Вопрос. В каких клетках изображено движение в противоположных направлениях (навстречу»)? Ответ. Движение «навстречу» изображено в клетках правой диагонали (I и IV). Вопрос. В каких клетках изображено движение в одном направлении («вдогонку»)? Ответ. Движение вдогонку изображено в клетках левой диагонали (11 и III). Вопрос. Сравните задачи (II и III). В каком случае быстрее нагонит один велосипедист другого? Почему? Ответ. В первом случае, так как в этом случае первоначальное расстояние между велосипедистами – 80 м. во втором случае – больше (160 м).
Мы описали беседу, основанную на качественных сравнениях:
(1—11), (IV—III), (I—IV). Однако в таком анализе можно пойти значительно дальше, проникая в глубинные связи, которые при обычной практике обучения на основе одинарных задач являются для мышления школьника недоступными. В процессе дополнительного обсуждения можно извлечь новые сведения.
Вопрос. Какова скорость сближения велосипедистов в (11) и (III) случаях? Ответ. Скорости сближения равные, так как в обоих случаях движение совершается вдогонку. Скорость сближения здесь равна 5+3=8 (м) за каждую секунду Вопрос. Через сколько секунд произойдет первая встреча в первой и четвертой задачах? Ответ. 80:2=40 (с); 160:2=80 (с). Вопрос. Через сколько секунд будут происходить последующие встречи? Через различное время или одно и то же время? Почему? Ответ. После первой встречи условия задач оказываются одинаковыми: в обоих случаях быстрейший должен нагнать медленного велосипедиста через (160+80):2=120 (с). Вопрос. Почему же здесь расстояние выросло до 160+80=240 (м)? Ответ . Потому что между данными двумя велосипедистами в момент встречи рас?