Курсовая работа: Состояние кормовой базы для свиней

n — число темпов роста.

Если произведение цепных темпов заменить соответствующим базисным темпом роста за весь изучаемый период, то получим формулу среднего темпа, имеющую следующий вид:

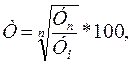(2.7)

где Т — средний темп роста;

Уn— абсолютный уровень конечного периода;

У0 — абсолютный уровень начального периода;

n — число периодов, равное числу лет минус единица (m-1).

Если абсолютная скорость прироста уровня динамического ряда характеризуется величиной абсолютного прироста, то относительная — темпом прироста.

Темп прироста — это отношение абсолютного прироста к уровню, принятому за базу. Темпы прироста, как и темпы роcта, могут быть выражены в форме коэффициентов и процентов. Коэффициент прироста показывает, на какую долю увеличился или уменьшился уровень по сравнению с базисным:

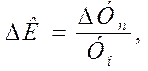(2.8)

где ΔК — коэффициент прироста уровня, выраженный в долях;

ΔУn— значение абсолютного прироста уровня;

У0 - уровень, принятый за базу.

Темп прироста, выраженный в процентах, показывает, на сколько процентов увеличился или уменьшился отчетный уровень по сравнению с базисным:

ΔТ=ΔК*100 (2.9)

Темпы прироста, как и темпы роста, могут быть рассчитаны базисным и цепным способами. Между темпами прироста и темпами роста существует непосредственная связь, т.е. если темп прироста выражен в процентах, то он на 100 % меньше темпа роста:

ΔТ==Т-100 (2.10)

Темпы прироста могут быть выражены положительными (+) и отрицательными (-) значениями. Положительное значение темпа указывает на рост отчетного уровня по сравнению с базисным, отрицательное — на его снижение В последнем случае говорят о темпе снижения.

Темпы прироста за весь промежуток времени в динамическом ряду могут быть охарактеризованы при помощи их среднего значения.

При расчете среднего темпа прироста можно исходить из значения среднего темпа роста:

ΔТ==Т-100, (2.11)

где ΔТ — средний темп прироста;

Т — средний темп роста.

При анализе динамического ряда необходимо выяснить, какими абсолютными значениями выражаются темпы роста, темпы прироста уровня, так как в некоторых случаях при снижении (замедлении) темпов роста абсолютный прирост может возрастать. Поэтому при анализе динамического ряда в статистике вычисляется абсолютное значение одного процента прироста (снижения).

Абсолютное значение одного процента прироста представляет собой отношение абсолютного прироста к темпу прироста, выраженному в процентах:

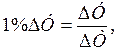(2.12)

После несложного преобразования формулы получим:

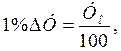(2.13)

Это означает, что абсолютное значение одного процента прироста (снижения) равно 0,01 базисного уровня.