Курсовая работа: Станок с кулисой

Тогда

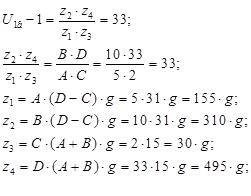
Пусть g = 1, тогда мы получим колеса наименьших радиусов.

Проверяем условие соосности (2):

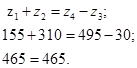
Условие выполняется.

Проверяем условие сборки (3):

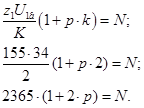
При p=1 N - целое число.

Условие выполняется.

Проверяем условие совместности (4):

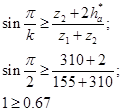
Следовательно, числа зубьев подобраны верно.

3.4. Графическое построение планетарного редуктора

После подбора чисел зубьев изображаем кинематическую схему механизма (масштаб чертежа: мм/м) в двух проекциях.

Радиусы колес определяются по формуле .

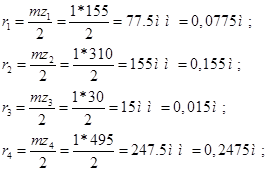
Для построения плана линейных скоростей на схеме редуктора отмечаем характерные точки: центр колеса 1(О) и колеса 4(), точки зацепления колес 1,2 (А) и 3,4 (С), а также ось сателлитов (В). Проводим прямоугольную систему координат, характерные точки переносим на вертикальную ось радиусов (). Горизонтальная ось называется осью линейных скоростей (). Определяем скорость точки А:

Из точки А проводим произвольный отрезок параллельно оси линейных скоростей. Конец отрезка отмечаем точкой . Затем находим масштаб скоростей: . Соединяя точки О и , получаем линию распределения линейных скоростей первого звена. Угол между вертикальной осью радиусов и линией распределения скоростей называем . Соединяем точки С и , таким образом получаем линию распределения линейных скоростей блока сателлитов, угол между вертикальной осью и отрезком С называем . Проводим из точки В отрезок до пересечения его с линией распределения линейных скоростей блока сателлитов. Точку пересечения называем . Соединяем точки и О, получаем линию распределения линейных скоростей водила. Угол между вертикальной осью и линией распределения линейных скоростей водила называем . Таким образом получаем план линейных скоростей механизма.

Для построения плана угловых скоростей проводим прямоугольную систему координат. Центр системы назовем точкой k. На вертикальной оси откладываем вниз произвольный отрезок kp. Из точки p проводим отрезки под углами ,, до пересечения с горизонтальной осью угловых скоростей (), соответственно обозначаем точки: 1, 2.3. и в. Таким образом мы получаем план угловых скоростей.

Находим : Найдем Теперь можно определить передаточное отношение .

5. Выводы

Подобраны числа зубьев, удовлетворяющие условиям соосности, сборки и соседства. Передаточное отношение проверено графически.