3) выравнивание по среднему абсолютному приросту:

Ў_i =У_i + Г (i-1) ,

где Ў_i - выровненное значение показателя;

У_i – начальное (базисное) значение уровня динамического ряда;

Г – средний абсолютный прирост (табл. 1.1-1.3).

4) выравнивание по среднему коэффициенту роста:

Ў_i =У_{i *} Ќ^{i -1} ,

где Ќ – средний коэффициент роста (табл. 1.1-1.3).

5) выравнивание по способу наименьших квадратов. Проводится с учетом предполагаемой тенденции изменения показателя. При линейной тенденции выравнивание идет с учетом уравнения:

Ў_i = a_o + a₁ t ,

где a_o и a₁ - параметры линейного уравнения;

t – порядковый номер года в динамическом ряду.

Используя математические преобразования, получаем следующие выражения для нахождения параметров линейного уравнения:

a_o = ΣY / n;

a₁ = ΣYt / Σt² .

Выравнивание динамических рядов различными методами приводятся в таблицах 2.1 –5.3. Для наглядного представления полученных результатов строятся графики и диаграммы. Как видно из графиков, отражающих выровненные значения показателей по всем методам, наиболее близки к фактическим значениям результаты выравнивания по способу наименьших квадратов.

Таблица 2.1

Выравнивание динамического ряда урожайности зерновых

методом скользящей средней и укрупнений интервалов

Годы	Урожайность зерновых, ц/га	Сумма за трехлетие	Выровненная урожайность	Среднее за трехлетие
1	8,0	Х	Х
2	8,5	24,3	8,1	8,1
3	7,8	28,2	9,4
4	11,9	30,3	10,1
5	10,6	36,4	12,1	12,1
6	13,9	38,9	13,0
7	14,4	46,6	15,5
8	18,3	52,3	17,4	17,4
9	19,6	58,7	19,6
10	20,8	58,6	19,5
11	18,2	60,9	20,3	20,3
12	21,9	62,7	20,9
13	22,6	66,5	22,2
14	22,0	70,5	23,5	23,5
15	25,9	х	Х

Динамика урожайности зерновых (У, ц/га)

Таблица 2.2

Выравнивание динамического ряда объема производственных затрат

методом скользящей средней и укрупнений интервалов

Годы	Производственные затраты, руб./га	Сумма за трехлетие	Выровненная урожайность	Среднее за трехлетие
1	100	х	Х
2	105	307,0	102,3	102,3
3	102	318,0	106,0
4	111	328,0	109,3
5	115	346,0	115,3	115,3
6	120	365,0	121,7
7	130	390,0	130,0
8	140	435,0	145,0	145,0
9	165	481,0	160,3
10	176	529,0	176,3
11	188	577,0	192,3	192,3
12	213	651,0	217,0
13	250	722,0	240,7
14	259	779,0	259,7	259,7
15	270	х	Х

Динамика производственных затрат (Х₁ , руб./га)

Таблица 2.3

Выравнивание динамического ряда количества атмосферных осадков

методом скользящей средней и укрупнений интервалов

Годы	Атмосферные осадки, мм/год	Сумма за трехлетие	Выровненная урожайность	Среднее за трехлетие
1	330	х	Х
2	200	656,0	218,7	218,7
3	126	626,0	208,7
4	300	636,0	212,0
5	210	709,0	236,3	236,3
6	199	619,0	206,3
7	210	655,0	218,3
8	246	601,0	200,3	200,3
9	145	583,0	194,3
10	192	493,0	164,3
11	156	638,0	212,7	212,7
12	290	696,0	232,0
13	250	760,0	253,3
14	220	840,0	280,0	280,0
15	370	Х	Х

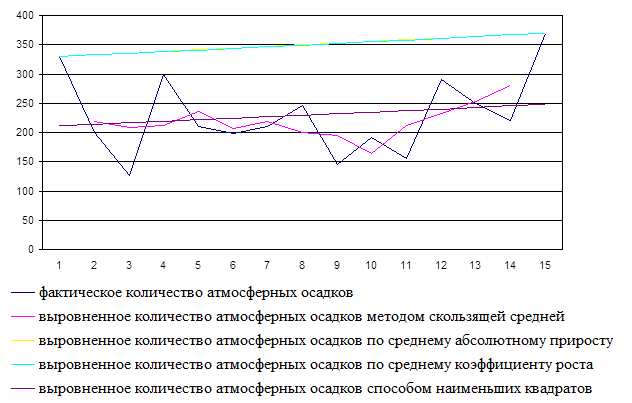
Динамика количества атмосферных осадков (Х₂ , мм/год)

Таблица 3.1

Выравнивание динамического ряда урожайности зерновых

по среднему абсолютному приросту

Ў _i =8,0+1,28*(i-1)

Годы	Фактическое значение урожайности зерновых	Выровненное значение урожайности зерновых
1	8,0	8,0
2	8,5	9,3
3	7,8	10,6
4	11,9	11,8
5	10,6	13,1
6	13,9	14,4
7	14,4	15,7
8	18,3	17,0
9	19,6	18,2
10	20,8	19,5
11	18,2	20,8
12	21,9	22,1
13	22,6	23,3
14	22,0	24,6
15	25,9	25,9

Таблица 3.2

Выравнивание динамического ряда производственных затрат

по среднему абсолютному приросту

Х_1i =100+12,14*(i-1)

Годы	Фактическое значение производственных затрат	Выровненное значение производственных затрат
1	100,0	100,0
2	105,0	112,1
3	102,0	124,3
4	111,0	136,4
5	115,0	148,6
6	120,0	160,7
7	130,0	172,9
8	140,0	185,0
9	165,0	197,1
10	176,0	209,3
11	188,0	221,4
12	213,0	233,6
13	250,0	245,7
14	259,0	257,9
15	270,0	270,0

Таблица 3.3

Выравнивание динамического ряда количества атмосферных осадков

по среднему абсолютному приросту

Х_2i =330+2,86*(I-1)

Годы	Фактическое значение атмосферных осадков	Выровненное значение атмосферных осадков
1	330,0	330,0
2	200,0	332,9
3	126,0	335,7
4	300,0	338,6
5	210,0	341,4
6	199,0	344,3
7	210,0	347,1
8	246,0	350,0
9	145,0	352,9
10	192,0	355,7
11	156,0	358,6
12	290,0	361,4
13	250,0	364,3
14	220,0	367,1
15	370,0	370,0

Таблица 4.1

Выравнивание динамического ряда урожайности зерновых

по среднему коэффициенту роста

У_i =8,0*1,088^i-1

Годы	Фактическое значение урожайности зерновых	Выровненное значение урожайности зерновых
1	8,0	8,0
2	8,5	8,7
3	7,8	9,5
4	11,9	10,3
5	10,6	11,2
6	13,9	12,2
7	14,4	13,2
8	18,3	14,4
9	19,6	15,7
10	20,8	17,0
11	18,2	18,5
12	21,9	20,1
13	22,6	21,9
14	22,0	23,8
15	25,9	25,9

Таблица 4.2

Выравнивание динамического ряда производственных затрат

по среднему коэффициенту роста

Х_1i =100,0*1,074^i-1

Годы	Фактическое значение производственных затрат	Выровненное значение производственных затрат
1	100,0	100,0
2	105,0	107,4
3	102,0	115,2
4	111,0	123,7
5	115,0	132,8
6	120,0	142,6
7	130,0	153,1
8	140,0	164,3
9	165,0	176,4
10	176,0	189,4
11	188,0	203,3
12	213,0	218,2
13	250,0	234,3
14	259,0	251,5
15	270,0	270,0

Таблица 4.3

Выравнивание динамического ряда количества атмосферных осадков

по среднему коэффициенту роста

Х_2i =330,0*1,008^i-1

Годы	Фактическое значение атмосферных осадков	Выровненное значение атмосферных осадков
1	330,0	330,0
2	200,0	332,7
3	126,0	335,4
4	300,0	338,2
5	210,0	341,0
6	199,0	343,8
7	210,0	346,6
8	246,0	349,4
9	145,0	352,3
10	192,0	355,2
11	156,0	358,1
12	290,0	361,0
13	250,0	364,0
14	220,0	367,0
15	370,0	370,0

Таблица 5.1

Выравнивание урожайности зерновых

способом наименьших квадратов

Годы	Фактическая урожайность зерновых, ц/га	Ранг года t	Уi *ti	t2	Выровненная урожайность зерновых, ц/га
1	8,0	-7	-56,0	49	7,2
2	8,5	-6	-51,0	36	8,5
3	7,8	-5	-39,0	25	9,8
4	11,9	-4	-47,6	16	11,1
5	10,6	-3	-31,8	9	12,4
6	13,9	-2	-27,8	4	13,7
7	14,4	-1	-14,4	1	15,0
8	18,3	0	0,0	0	16,3
9	19,6	1	19,6	1	17,6
10	20,8	2	41,6	4	18,9
11	18,2	3	54,6	9	20,2
12	21,9	4	87,6	16	21,5
13	22,6	5	113,0	25	22,8
14	22,0	6	132,0	36	24,1
15	25,9	7	181,3	49	25,3
Итого	244,4	0,0	362,1	280,0	х

Динамика роста урожайности зерновых

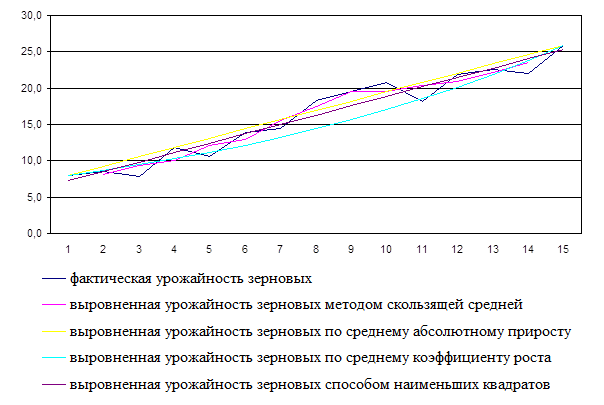
Таблица 5.2

Выравнивание производственных затрат

способом наименьших квадратов

Годы	Фактические производственные затраты, руб./га	Ранг года t	Уi *ti	t2	Выровненная производственные затраты, руб/га
1	100	-7	-700,0	49	72,2
2	105	-6	-630,0	36	85,2
3	102	-5	-510,0	25	98,1
4	111	-4	-444,0	16	111,1
5	115	-3	-345,0	9	124,1
6	120	-2	-240,0	4	137,0
7	130	-1	-130,0	1	150,0
8	140	0	0,0	0	162,9
9	165	1	165,0	1	175,9
10	176	2	352,0	4	188,8
11	188	3	564,0	9	201,8
12	213	4	852,0	16	214,8
13	250	5	1250,0	25	227,7
14	259	6	1554,0	36	240,7
15	270	7	1890,0	49	253,6
Итого	2444,0	0,0	3628,0	280,0	х

Динамика роста производственных затрат

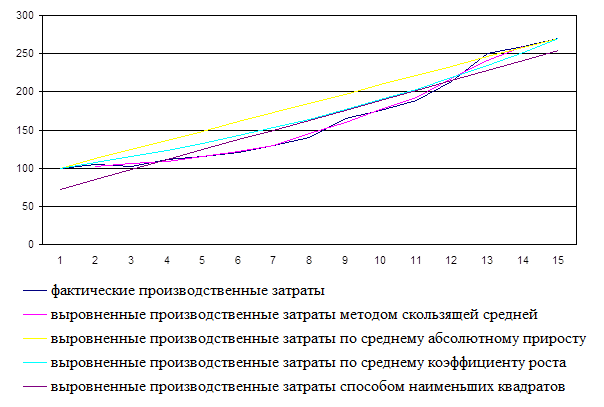
Таблица 5.3

Выравнивание количества атмосферных осадков

способом наименьших квадратов

Годы	Фактические атмосферные осадки, мм/год	Ранг года t	Уi *ti	t2	Выровненные атмосферные осадки, мм/год
1	330	-7	-2310,0	49	211,1
2	200	-6	-1200,0	36	213,8
3	126	-5	-630,0	25	216,4
4	300	-4	-1200,0	16	219,0
5	210	-3	-630,0	9	221,7
6	199	-2	-398,0	4	224,3
7	210	-1	-210,0	1	227,0
8	246	0	0,0	0	229,6
9	145	1	145,0	1	232,2
10	192	2	384,0	4	234,9
11	156	3	468,0	9	237,5
12	290	4	1160,0	16	240,2
13	250	5	1250,0	25	242,8
14	220	6	1320,0	36	245,4
15	370	7	2590,0	49	248,1
Итого	3444,0	0,0	739,0	280,0	х

Динамика роста количества атмосферных осадков

ГЛАВА 2. Вариационные ряды

2. 1. Построение и анализ вариационных рядов

Первым шагом систематизации материалов статистического наблюдения является подсчет числа единиц, обладающих тем или иным признаком. Расположив единицы в порядке возрастания или убывания их количественного признака и подсчитав число единиц с конкретным значением признака, получаем вариационный ряд. Другими словами, вариационный ряд характеризует распределение единиц определенной статистической совокупности по какому-либо количественному признаку. Вариационный ряд – это ряд чисел, показывающий, каким образом числовые значения признака связаны с их повторяемостью. Количество повторяемости – частота или веса вариантов (F).

При кадастровой оценке земель используется сплошной метод, т. е. исходные данные берутся по всем хозяйствам земельно-оценочного района и не могут быть нормально распределены из-за различного уровня интенсивности сельскохозяйственного производства колхозов и совхозов. Поэтому нормально распределены должны быть результативные показатели, отнесенные к единице производственных факторов.

Анализ вариационного ряда начинают с определения показателей вариации:

1) размах вариации (R) характеризует колебания максимального и минимального значения переменной:

R = X_max – X_min ;

2) среднее квадратическое отклонение (σ) наиболее объективно характеризует колеблемость:

σ = ,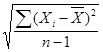

где – среднеарифметическое значение переменных ряда;

3) нормированное отклонение вариационного ряда проверяет нормальность распределения переменных в нем:

t = ;

Нормальное распределение – распределение, описывающееся плотностью. Кривая нормального распределения – кривая, изображающая плотность распределения. Она выражается формулой Гаусса-Лапласа:

.

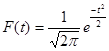Асимметрия – мера косости распределения. Этот показатель характеризует горизонтальное отклонение кривой F(t) от кривой нормального распределения (влево или вправо):

.

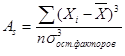Эксцесс – мера крутости распределения. Характеризует вертикальное отклонение кривой нормального распределения:

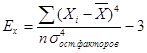
2. 2 Статистическая группировка земельно-кадастровых показателей

и построение статистических таблиц

При обработке статистических материалов возникает необходимость выделения однородных групп, типов, а затем уже описание этих групп определенными количественными характеристиками. Расчленение совокупности на группы, однородные по какому-либо признаку, называется группировкой. Для ее проведения необходимо определить те характеристики (группировочные признаки), по которым она будет проводиться, и их значений, отделяющих одну группу от другой (интервалы группировки).

В данной работе группировка будет проводиться по таким важным экономическим показателям, как урожайность, стоимость валовой продукции и чистого дохода на 1 га сельскохозяйственных угодий. Для этого в таблицах 7.1 – 7.5 производится расчет валовой продукции, чистого дохода и производственных затрат по всем культурам в 20 хозяйствах с использованием следующих формул:

- валовая продукция: ,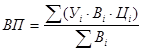

где В_i – удельный вес культуры в данном хозяйстве;

У_i – урожайность культуры;

Ц_i – кадастровая цена за 1 ц продукции.

- производственные затраты: ,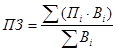

где П_i – производственные затраты по i-ой культуре.