Курсовая работа: Статистическая оценка деятельности предприятия строительной отрасли
Значение параметров уравнения параболы рассчитываются следующим образом:
, 
,
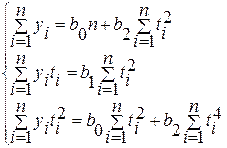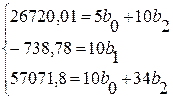5b0 = 26720,01– 10b 2 b 2 = 259,413
57071,8 = 2(26720,01 – 10b 2 ) + 34b 2 
,
Таким образом, 
, 
, 
Уравнение параболы имеет вид:
Так как основной целью аналитического выравнивания является экстраполяция, следовательно, требуется выяснить какое из уравнений прямой или параболы – лучше описывает тенденцию динамики среднесписочной численности работников, для этого рассчитаем среднюю квадратическую ошибку уравнения тренда и коэффициент вариации:
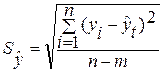, (1.15)
где n – число уровней ряда, m – число параметров в уравнении тренда ( для прямой m=2), 
- соответственно фактическое и расчётное значения уровней динамического ряда.
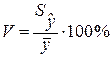
где 
- средний уровень динамического ряда. (1.16)
Для уравнения прямой:
n = 5, m = 2
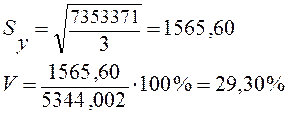
Для уравнения параболы:
n = 5, m = 3
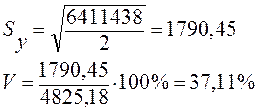
Поскольку коэффициент вариации для уравнения параболы больше, чем для уравнения прямой, то уравнение прямой более точно описывает основную тенденцию динамики ввода в действие жилья.
Аналогичные расчеты аналитического выравнивания по уравнению прямой и параболы для среднемесячной заработной платы представлены в таблицах 1.9, 1.10
Таблица 1.9 Аналитическое выравнивание среднемесячной заработной платы по прямой
|
годы |
Среднемесячная заработная плата, грн |
ti |
Yi*ti |
ti^2 |
Yt |
К-во Просмотров: 691
Бесплатно скачать Курсовая работа: Статистическая оценка деятельности предприятия строительной отрасли
|