Курсовая работа: Статистические методы анализа финансовых результатов деятельности предприятий

Тогда 61,4 – 15,4

i = 5 = 9,2

Отсюда путём прибавления величины интервала к минимальному уровню признака в группе получим следующие группы предприятий по размеру затрат на приозводство и реализацию продукции (табл.1).

Таблица 1.

Распределение предприятий по размеру затрат.

№ п/п	Группы предприятий по размеру затрат, млн. руб.	Число предприятий
		В абсолютном выражении, ед.	В относительных единицах,%
1	15,4 – 24,6	5	16,7
2	24,6 – 33,8	12	40,0
3	33,8 – 43,0	7	23,3
4	43,0 – 52,2	4	13,3
5	52,2 – 61,4	2	6,7
Итого	30	100,0

Данные группировки показывают, что около 44% предприятий имеют затраты свыше 33,8 млн. руб.

2. Построим графики полученного ряда распределения. Графически определим значения моды и медианы.

1) Построим гистограмму и определим значение моды (рис.1). Первоначально по наибольшей частоте признака определим модальный интервал. Наибольшее число предприятий – 12 – затрачивают на производство и реализацию продукции сумму в интервале 24,6-33,8 млн. руб., который и является модальным. Для определения значения моды правую вершину модального прямоугольника соединим с верхним правым углом предыдущего прямоугольника, а левую вершину – с верхним левым углом предшествующего. Абсцисса точки пересечения этих прямых будет мода. Мо ≈ 31 млн. руб. – наиболее часто встречающееся значение признака.

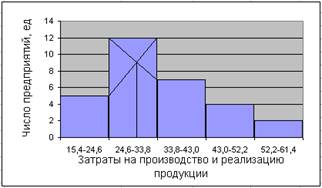
Рис.1. Гистограмма распределения предприятий по затратам на производство и реализацию продукции.

2) Для определения значения медианы построим кумуляту распределения предприятий по затратам на производство и реализацию продукции (Рис.2).

Определим медианный интервал, таким интервалом очевидно будет интервал затрат 24,6-33,8 млн. руб., так как его кумулятивная частота равна 17 (5+12), что превышает половину суммы всех частот (30: 2=15).

Далее определим ординаты накопленных частот в пределах 24,6-33,8, это будет у1 = 29, у2 = 40 и у3 = 32. Найдём середину промежутка ординат накопленных частот в пределах 24,6-33,8:

у1+у2+у3 29+40+32

Уср = 3 = 3 = 33.

Абсцисса середины промежутка есть медиана. Ме ≈ 33.

Полученный результата говорит о том, что из 30 предприятий 15 имеют затраты на производство и реализацию продукции менее 33 млн. руб., а 15 предприятий – более.

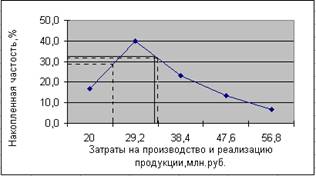
Рис.2. Кумулята распределения предприятий по затратам на производство и реализацию продукции.

3. Основные характеристики интервального ряда распределения. Вспомогательные расчёты представлены в таблице 1.1.

Таблица 1.1.

№п/п	Затраты на производство и реализацию продукции, млн. руб., х	Число предприятий, f	Середины интервалов х	х*f	(x-xср) 2	(x-xср) 2*f
1	15,4 - 24,6	5	20	100	199,00	994,9902
2	24,6 - 33,8	12	29,2	350,4	24,08	288,90
3	33,8 - 43,0	7	38,4	268,8	18,43	129,03
4	43,0 - 52,2	4	47,6	190,4	182,07	728,28
5	52,2 - 61,4	2	56,8	113,6	514,99	1029,97
Итого	30	192	1023,2	938,5636	3171,18
Среднее	34,11
Среднее квадратическое.	10,28
Коэффициент вариации	30,14

1) Средняя арифметическая ∑х*f

хср = ∑f

1023,2

хср = 30 = 34,1 (млн. руб)

Соотношение между модой, медианой и средней характеризуют форму распределения. Если IМо-хсрI ≈ 3*IМе-хсрI

I31 – 34,1I ≈ 3*I33 – 34,1I