Курсовая работа: Статистические методы оценки значимости компонент педагогической системы учителя
где S – наблюдаемая сумма квадратов отклонений, k – количество экспертов, n – число членов выборки (факторов), тогда W = 0,821.
Проверим значимость W. Если ранжировки независимы, то величина ![]() имеет примерно F -распределение с числом степеней свободы
имеет примерно F -распределение с числом степеней свободы ![]() (v1 = 9),
(v1 = 9), ![]() , v2 = 34. Находим, что величина
, v2 = 34. Находим, что величина ![]() значима для уровня
значима для уровня ![]() . Следовательно, можно утверждать, что существует неслучайная согласованность мнений экспертов: их мнения согласуются.
. Следовательно, можно утверждать, что существует неслучайная согласованность мнений экспертов: их мнения согласуются.
Представляет определенный интерес проанализировать согласованность и взаимную корреляцию оценок отдельных пар экспертов. Для этого вычислим коэффициенты ранговой корреляции Спирмена, определяемые следующим образом:
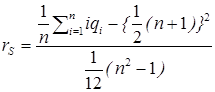 ,
,
отсюда
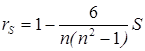
Проанализируем ![]() для первых двух мнений экспертов. Первый эксперт проанализировал компоненты учебной деятельности в порядке возрастания их значимости следующим образом:
для первых двух мнений экспертов. Первый эксперт проанализировал компоненты учебной деятельности в порядке возрастания их значимости следующим образом:
![]()
Соответственно, в порядке возрастания рангов можно записать:
![]() 1 2 3 4 5 6 7 8 9 10
1 2 3 4 5 6 7 8 9 10
Этим рангам соответствуют ранги 2-го эксперта:
![]() 1 2 3 4 5 8 6 7 9 10
1 2 3 4 5 8 6 7 9 10
Тогда для пары первый-второй эксперт ![]() .
.
По таблицам распределения Стьюдента для n = 10. и ![]() верхнее критическое значение коэффициента Спирмена, равное 0,745. Так как найденное значение
верхнее критическое значение коэффициента Спирмена, равное 0,745. Так как найденное значение ![]() меньше критического, то «нуль-гипотеза» (Н0 ) отклоняется, и значит мнения первого и второго экспертов коррелированны.
меньше критического, то «нуль-гипотеза» (Н0 ) отклоняется, и значит мнения первого и второго экспертов коррелированны.
Вообще говоря, можно было бы сделать вывод о корреляции мнений и по другому методу.
Дело в том, что если ![]() больше нуля, то корреляция положительная, а если
больше нуля, то корреляция положительная, а если ![]() меньше нуля – она отрицательная.
меньше нуля – она отрицательная.
Для корреляции мнений 1-го и 3-го экспертов ![]() ,
, ![]() , то есть мнения 1-го и 3-го экспертов коррелированны.
, то есть мнения 1-го и 3-го экспертов коррелированны.
Для 1-го и 4-го экспертов ![]() ,
, ![]() , то есть мнения 1-го и 4-го экспертов коррелированны.
, то есть мнения 1-го и 4-го экспертов коррелированны.
Для 1-го и 5-го экспертов ![]() ,
, ![]() , то есть мнения 1-го и 5-го экспертов коррелированны.
, то есть мнения 1-го и 5-го экспертов коррелированны.
Помимо коэффициента ранговой корреляции Спирмена при статистической обработке результатов исследований пользуются коэффициентом ранговой корреляции Кендалла.
В соответствии с этим методом определения корреляции рассмотрим упорядоченные по Y ранги: 1, 2, 3, …, n и соответствующие им ранги X: q 1 , q 2 , q 3 , …, q n .
Коэффициент ранговой корреляции Кендалла вычисляется по формуле:
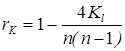
или по эквивалентной формуле:
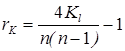 ,
,
где ![]() называется статистикой Кендалла,
называется статистикой Кендалла, ![]() - сумма инверсий для рангов X.
- сумма инверсий для рангов X.
![]() .
.
Если ![]() , то корреляция положительная, а если
, то корреляция положительная, а если ![]() - отрицательная.
- отрицательная.
Анализ корреляции мнений экспертов позволяет получить: