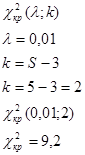Рисунок 2 – Гистограмма и полигон частот для x

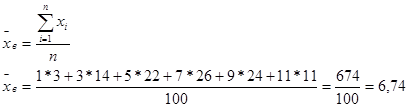
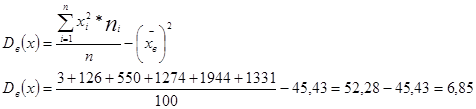
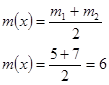
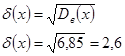
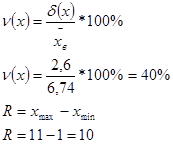
Задание выполняется с помощью макроса, текст которого приведен в приложении А.

Задание №3

С надежностью определить доверительный интервал для y и необходимый объем выборки для вдвое меньшей предельной выборки.

Доверительным интервалом называется интервал, который с надежностью покрывает оцениваемый интервал.

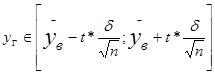, где

– точность оценки,

– объем выборки,

– значение функции Лапласа

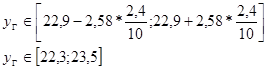
Определяем необходимый объем выборки для вдвое меньшей предельной ошибки.

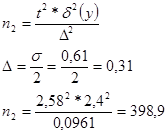
Задание выполняется с помощью макроса, текст приведен в приложение Б.

Задание №4

Предполагая распределение количества вырабатываемых за смену изделий одним рабочим – y нормальным, вычислить теоретическую частоту. Проверить значимость расхождения теоретических и эмпирических частот по критерию Пирсона на 1% уровня значимости и сделать вывод о согласовании с опытными данными гипотезы, что количество вырабатываемых изделий за смену (y) распределено по нормальному закону.

Критерием согласия называется критерий проверки гипотезы о предполагаемом законе неизвестного распределения. С этой целью будем сравнивать эмпирические (наблюдаемые) и теоретические значения. Допустим, что в предположенном нормальном распределении вычислены теоретические частоты (). При уровне значимости требуется проверить нулевую гипотезу (): генеральная совокупность распределена нормально. В качестве критерия проверки нулевой гипотезы принимаем случайную величину .

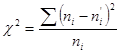
Эта величина случайная, так как в различных опытах она принимает различные заранее неизвестные значения.

Правило : для того чтобы при заданном уровне значимости проверить нулевую гипотезу, надо сначала вычислить теоретические частоты, а затем наблюдаемые значения критерия.

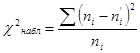
По таблице критических точек распределения , по заданному уровню значимости и числу степеней свободы , найти критическую точку . Если – нет оснований отвергать нулевую гипотезу, если

, то нулевая гипотеза отвергается.

Таблица 6 – Данные для проверки расхождения теоретических и эмпирических частот

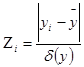18	2,04	0,05	8	4,2
20	1,21	0,19	16	15,8
22	0,4	0,37	18	30,8
24	0,5	0,35	39	29,2
26	1,3	0,17	19	14,2
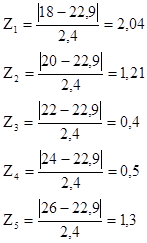
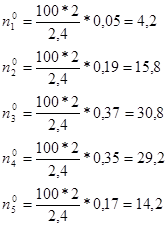
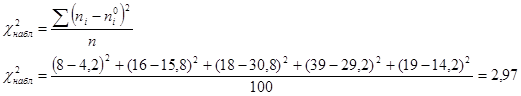