Курсовая работа: Строительство промышленного здания 2

Каноническое уравнение метода перемещений имеет вид:

где c_din - коэффициент учитывающий пространственную работу каркаса здания при крановых нагрузках; - сумма реакций несмещаемого верха колонн от внешнего воздействия;

-сумма реакций в фиктивной связи основной системы от единичного перемещения; - искомое горизонтальное перемещение верха колонны.

Основную систему подвергают единичному воздействию неизвестного
и вычисляют реакции верхнего конца двухветвевых колонн по формулам:

Суммарная реакция в фиктивной связи основной системы:

Затем основную систему постепенно загружают постоянными и временными нагрузками, которые вызывают в колоннах соответствующие реакции и изгибающие моменты. Значения реакций несмещаемого верха колонн от внешнего воздействия также определяются по формулам, приведенным в прил. 12.

Действительную (упругую) реакцию верха каждой колонны рамы от: любой нагрузки находят по формуле:

Далее прикладывают к i-той колонне соответствующую нагрузку и реакцию R_{ei ,} вызванную этой нагрузкой, и находят внутренние усилия М, N и Q в сечениях колонн как в консоли, защемленной в фундаменте.

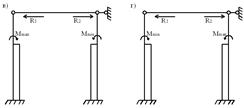
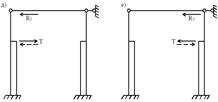
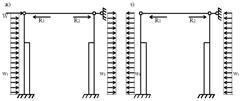
Усилия в колоннах поперечной рамы от постоянной нагрузки (рис.4,б).

В верхней части колонны продольная сила N_п =653 кН приложена с эксцентриситетом e₁ =0,15м. Изгибающий момент M₁ =N_п e₁ =

в подкрановой части колонны, кроме силы N_п , приложенной с эксцентриситетом
е₂ =0,3 м действуют: расчетная нагрузка от веса подкрановой

балки и подкранового пути N_п.б. =120 кН с е₄ =0,4 м; расчетная нагрузка от
надкрановой части колонны N_к ^в =34,5 кН с эксцентриситетом е₂ =0,3 м;
расчетная нагрузка от стеновых панелей N_ст =191 кН с эксцентриситетом
е₃ =0,75м.

Вычисляют реакцию верхнего конца колонны по оси А (левой) по формуле

Рис. 4. К определению реакций в колоннах от нагрузок.

Согласно принятому в расчете правилу знаков реакция, направленная вправо, положительна. Реакция правой колонны R₂ =5,2кН. Суммарная реакция связей в основной системе

R_ip =ΣRi=-5,2+5,2=0 (при этом из канонического уравнения следует, что Δ₁ =0).

Упругая реакция колонны по оси A:

Изгибающие моменты в сечениях колонны (нумерация сечений показана на рис.4,а) равны: