Курсовая работа: Структурный синтез активных фильтров ВЧ и СВЧ диапазонов

Снятие указанных структурных противоречий требует применения дополнительной общей отрицательной обратной связи и, следовательно, мультидифференциальных ОУ.

4. Синтез структур R -звеньев с дополнительными частотнозависимыми цепями

Как отмечалось выше, увеличение в R-фильтрах максимального уровня выходного напряжения связано с уменьшением коэффициента сдвига частоты полюса b_z , что приведет к увеличению собственного шума схемы. Кроме этого, особенность схемотехнических решений ОУ в СВЧ диапазоне не позволяет использовать высокоомные резисторы в цепях местных и общей обратных связей, что существенно увеличивает потребляемый ток. Следует также отметить, что в этом же диапазоне частот подложка, занимаемая RC-цепью первого порядка, не превышает геометрическую площадь ОУ. Таким образом, и это можно показать достаточно строго, повышение многих показателей качества возможно путем использования в качестве частотозадающих цепей не только частотных свойств скорректированных ОУ, но и традиционных RC-цепей.

Предварительно отметим, что базовый вывод о невозможности построения ФВЧ и заграждающих фильтров в этом случае также сохраняется. Таким образом, для построения звеньев как полосового фильтра, так и фильтра нижних частот необходимо использовать один ОУ и RC-цепь первого порядка. Тогда для звена полосового типа:

(37)

а для ФНЧ

(38)

Принципиальные схемы таких звеньев приведены на рис. 4.

а) б)

Рис. 4. Принципиальные схемы звеньев второго порядка

с дополнительными частотозадающими цепями:

а) ФНЧ; б) ПФ

Анализ схем приводит к следующим результатам:

– для ФНЧ

, (39)

; (40)

– для звена ПФ

, (41)

. (42)

Таким образом, уровни динамических диапазонов звеньев определяются следующими соотношениями:

, (43)

. (44)

Поэтому

(45)

звеньев с дополнительными цепями в раз больше, чем в R-фильтрах.

В качестве примера реализации звена второго порядка с единственным конденсатором (RC/2-звенья) рассмотрим полосовой фильтр на базе ОУ с указанными в табл. 2 параметрами. На рис. 5 приведены результаты моделирования схемы для различной добротности. Как видно из соотношений (41), это достигается изменением постоянной времени RC-цепи (рис. 4б) в относительно широких пределах.

Для указанного набора параметров полоса звена – и Q выполнено моделирование схем во временной области (рис. 6, 7, 8) при подаче различных уровней гармонического сигнала в полосе пропускания. Анализ длительности переходных процессов показывает, что схема остается линейной при условии, что выходное ее напряжение не превышает граничное напряжение ОУ (табл. 2). Однако различия скорости нарастания выходного напряжения () ограничивают максимально достижимое выходное напряжение схем. Основные характеристики звена приведены в табл. 4.

электронный усилитель частотный операционный

Таблица 4

Основные характеристики RC /2-звена полосового типа

	, (%)	, (МГц)	, (%)	Q	Q, (%)	, (мВ)	, (дБ)
30,55	1	364	10	10,8	49	82	45
12,74	45	484	6,2	6,66	37	82	40
4,73	56	657	13,3	3,55	14	100	36
Примечание. – гарантированное затухание сигнала в полосе заграждения фильтра.

Приведенные в табл. 4 погрешности реализации основных параметров связаны, как показывают дополнительные исследования, с влиянием паразитной входной емкости и вторым полюсом промежуточного каскада ОУ. Это, в частности, подтверждается результатами моделирования схемы звена ФНЧ (рис. 4а), где в силу параллельности основного каскада обратной связи аналогичные отклонения достигают 100 %, а влияние выходного сопротивления существенно уменьшает гарантированное затухание схемы в полосе заграждения.

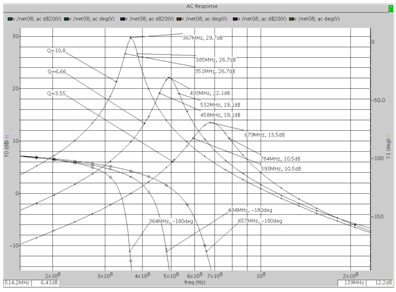
Рис. 5. Частотные характеристики RC/2-звена полосового типа

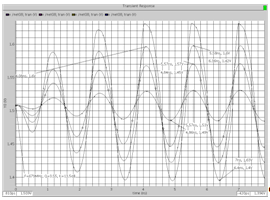
Рис. 6. Реакция схемы при Q=3,55 на различные уровни

входного гармонического воздействия

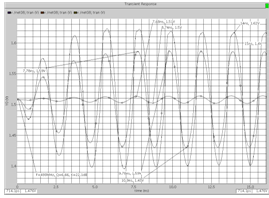
Рис. 7. Реакция схемы при Q = 6,66 на различные уровни

входного гармонического воздействия

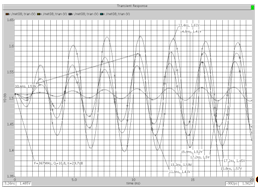
Рис. Реакция схемы при Q = 10,8 на различные уровни

входного гармонического воздействия

5. Синтез ФНЧ третьего порядка с дополнительными RC -цепями

Фильтры нижних частот в СВЧ диапазоне образуют отдельный и важный в практическом отношении класс устройств частотной селекции. Достаточно отметить каналообразующие фильтры при синхронной обработке сложных радиотехнических сигналов. В этом случае необходимо не только подавление амплитуд суммарных гармонических составляющих, но и обеспечение линейной фазочастотной характеристики в рабочем диапазоне частот. В общем случае такие фильтры могут быть построены путем каскадирования звеньев второго и первого порядков, однако в ряде практически важных устройств (например, СФ блоков) относительно высокие качественные показатели обеспечиваются применением только одного ОУ с дополнительной RC-цепью второго порядка. При таком подходе получим

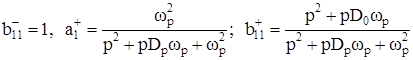, (46)

где D₀ , D_p – затухание нуля и полюса пассивной цепи.

Структура локальной передачи имеет относительно простую физическую трактовку. Коэффициент при операторе p обеспечивает, как и в обычных RC-звеньях, компенсацию потерь в пассивной цепи и, следовательно, потенциальное увеличение добротности (Q). Именно такие свойства цепи без дополнительных структурных мер в реальных фильтрах и приводят к пропорциональному Q сдвигу граничной частоты, обусловленному влиянием площади усиления ОУ. Для исключения этой зависимости в структуре используется дополнительный член p² , который и позволяет получить необходимые для решения общей задачи параметрические степени свободы. Принципиальная схема такого звена показана на рис. 9.

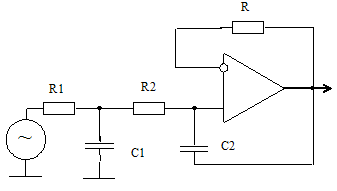
Рис. 9. Принципиальная схема ФНЧ третьего порядка R2C/3 типа

Анализ схемы позволяет определить набор базовых передаточных функций:

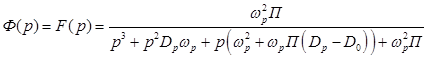, (47)

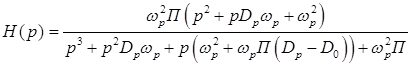. (48)

Введем нормировку оператора для перехода к НЧ-прототипу

(49)

и коэффициент сдвига частоты

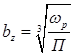, (50)

получим

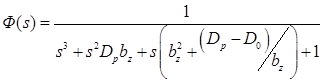, (51)

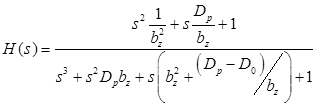. (52)

В диапазоне рабочих частот для АЧХ без явно выраженных пульсаций

, (53)

а

(54)

Таким образом, динамический диапазон схемы определяется следующим соотношением:

(55)

и в основном зависит от возможности минимизации численного значения затухания полюса D_p .

Оценим возможность создания на базе настоящей схемы ФНЧ с линейной фазовой характеристикой. Решение классической аппроксимационной задачи приводит к следующему положению полюсов передаточной функции (51):

. (56)

Следовательно, ее коэффициенты должны принимать значения

, (57)

при этом граничная частота ω₀ будет определяться частотой полюса пассивной цепи ω_р и площадью усиления П. Для решения задачи необходимо найти соотношения между резистивными и емкостными элементами схемы. Учитывая, что

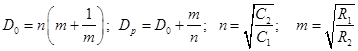, (58)