Курсовая работа: Суммирующий счетчик
На рисунке 3.5.2, б представлено условное изображение 4-разрядного счетчика. На счетный С вход поступают импульсы. Логическая единица на входе К сбрасывает все разряды счетчика в ноль. По входам предварительной установки D0 – D3 в счетчик может быть записано число, его значение должно сопровождаться логической единицей на входе разрешения V. Число, занесенное в счетчик, фиксируется на его выходах двоичным кодом с «весами» разрядов 1-2-4-8. На выходе P+ появляется логическая единица с поступлением на вход 16-го импульса, т. е. вслед за тем, как предыдущими 15-ю импульсами все разряды счетчика были установлены в единицу.
Суммирующий счетчик функционирует по правилам сложения двоичных чисел. Это легко проследить по временной диаграмме, изображенной на рисунке 3.5.2, где крестиками отмечены переключающие перепады 1/0.
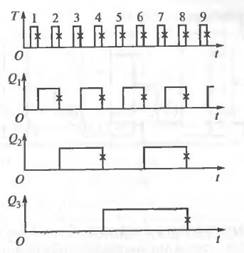
Рисунок 3.5.2. Временная диаграмма работы суммирующего счетчика.
Из временных диаграмм можно сделать следующие выводы:
- с наибольшей частотой переключается входной триггер счетчика;
- частота импульсов на выходе каждого триггера вдвое меньше, частоты импульсов на его входе, а nразрядов счетчика делят частоту входных импульсов в 2n раз, таким образом, счетчик является делителем числа входных импульсов с коэффициентом деления (пересчета), равным емкости счетчика Ксч ;
- при поступлении на вход суммирующего счетчика 2n импульсов он переполняется: все триггеры устанавливаются в 0 (счетчик обнуляется);
- максимальное число, которое может содержать счетчик, на единицу меньше его емкости N = Ксч – 1 = 2n – 1;
- в момент, предшествующий переключению очередного разряда, все предыдущие разряды счетчика находятся в состоянии 1.
Если в счетчике использованы триггеры, переключающиеся перепадом 0/1, то вход последующего триггера нужно соединить с инверсным выходом предыдущего, на котором формируется этот перепад, когда по основному выходу триггер переключается из 1 в 0. [1]
4. Логическое моделирование
4.1 Моделирование TV-триггера
триггер суммирующий счетчик
По заданию, необходимо использовать динамический TV-триггер, в качестве базисного. Для этого, модифицируем схему стандартного динамического JK триггера, превратив его в T-триггер, и добавив ему асинхронные входа R и V (сброс и принудительное хранение). В итоге, собранный триггер будет выглядеть следующим образом:
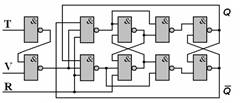
Рисунок 4.1.1. Динамический TV-триггер.
Проведем логическое моделирование TV-триггера в Orcad:
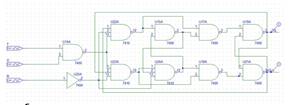
Рисунок 4.1.2. Схема TV-триггера в Orcad.
Результат логического моделирования:
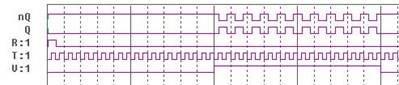
Рисунок 4.2.3. Диаграмма переключения TV-триггера.
Таблица 4.1.1. Таблица истинности TV-триггера.
| V | T | Qn+1 |
| 0 | 0 | Qn |
| 0 | 1 | Qn |
| 1 | 0 | Qn |
| 1 | 1 | ⌐ Qn |
4.2 Моделирование суммирующего счетчика
Проведем логическое моделирование в Orcad:
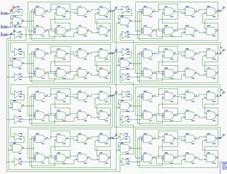
Рисунок 4.2.1. Схема суммирующего счетчика в Orcad.
Результат логического моделирования:

Рисунок 4.2.2. Диаграмма переключения суммирующего счетчика.
Таблица 4.2.1. Таблица истинности суммирующего счетчика
| Номер состояния | Q1 | Q2 | Q3 | Q4 | Q5 | Q6 | Q7 | Q8 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 6 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 7 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 8 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 9 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 10 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 11 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| 12 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| 13 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 14 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 15 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| 16 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| 17 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 18 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 19 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| … | … | … | … | … | … | … | … | … |
| 250 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 251 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 252 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 253 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 254 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 255 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 256 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |