Курсовая работа: Turbo Pascal
readkey;
ClrScr;
writeln;
writeln(' *******************************************************');
writeln(' * Вектор из средних арифметических значений элементов *');
writeln(' * столбцов результирующей матрицы. *');
writeln(' *******************************************************');
sred_arifm(n, u, vect);
writeln; write(' ');
for i:=1 to n do
write(' ',vect[i]:5:2);
writeln;
readkey;
end.
Задание 2
1. Анализ задания и математическая постановка задачи
При решении поставленной задачи необходимо выполнить следующие действия:
1. Ввод исходных данных.
2. Нахождение значения определённого интеграла с использованием метода прямоугольников.
3. Вывод результатов.
При численном интегрировании вместо кривой подынтегральной функции используют заменяющие (аппроксимирующие) её кривые или ломаные линии, для которых вычисление ограниченной ими площади производится в соответствии с достаточно несложными формулами.
Принцип метода прямоугольников состоит в том, что исходный отрезок разбивается на достаточно малые части:
a= x1 < x2 < x3 <…< xn-1 < xn =b; h= xk -xk-1 ;
площадь каждой такой части (прямоугольника): Sk =h*f(xk );
соответственно площадь всей фигуры, образованной из n-1 таких прямоугольников: S= S1 +S2 +…+ Sn-2 + Sn-1 .Величина S является приближённым значением определённого интеграла, она приближается к истинному значению при увеличении числа n.
Погрешность данного метода определяется абсолютным значением разности приближённых значений определённого интеграла при различных n. Если эта разность меньше требуемой погрешности, то необходимая точность достигнута, и дальнейшее увеличение n не требуется.
2. Разработка схемы алгоритма и её описание
По результатам анализа задания можно составить укрупненную схему алгоритма последовательной структуры:
 | ||||
Полный алгоритм:
| ||||||
| ||||||
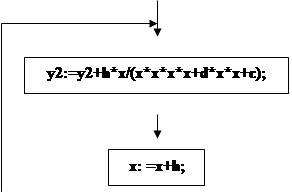 | ||
 Нет Нет |
| Да |