Курсовая работа: Ультразвуковой контроль ближней подступной части оси колесной пары
При рассеянии поток звуковой энергии остается звуковым, но уходит из направленно-распространяющегося пучка. Металлы, применяемые на практике, имеют зернистую структуру. Размеры зерен зависят от химического состава, вида механической и термической обработки деталей. Затухание волн в них обуславливается двумя факторами: рефракцией и рассеянием вследствие анизотропии механических свойств. В результате рефракции фронт волны отклоняется от прямолинейного направления распространения, и амплитуда принимаемых сигналов резко падает. Кроме того, волна, падающая на поверхность границы зерна, испытывает частичное отражение и преломление ультразвука и трансформацию, что и определяет механизм рассеяния. Рассеяние в отличие от фракции приводит не только к ослаблению сигнала, но и к образованию шумов. Явление рассеяния тем сильнее, чем больше средний размер зерна по сравнению с длиной ультразвуковой волны.
Явления поглощения и рассеяния ослабляют ультразвуковую волну тем сильнее, чем больший путь в среде она проходит.
1.4 Отражение, преломление и трансформация ультразвуковых
волн
Если на пути распространения ультрозвуковой волны встречается другая среда, то одна часть энергии проходит во вторую среду, а другая – отражается в первую среду.
На границе раздела происходят основные явления: отражение, преломление и трансформация волн. Преломление – это изменение направления распространения волны, а трансформация – преобразование (превращение) волны одного типа в другой. Переходы исходного состояния волны в другие связаны энергетическими соотношениями, определяемыми, главным образом, типом падающей волны, углом ее падения и соотношением удельных акустических сопротивлений обеих сред.
В общем случае, если волна падает на границу раздела двух твердых сред под углом β из первой среды во вторую, то в обеих средах возникают четыре волны (рисунок 3): в каждой по две волны продольного и поперечного типа.
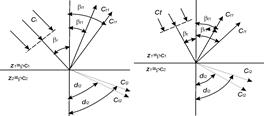
Рисунок 3 - Падение ультразвуковой волны на границу раздела двух сред
Причем при облучении продольной «l» - волной образуются отраженные продольная «l1 » и поперечная «t1 », возникшая в результате явления трансформации, и две преломленные волны «l2 » и «t2 », из которых последняя трансформированная (рисунок 3,а). При облучении поперечной волной также образуются отраженные волны «l1 » и «t1 », но трансформированная волна уже продольная, и две преломленные – «l2 » и «t2 , где волна продольного типа «l2 » также трансформированная (рисунок 3,б).
Углы отражения βe 1 , βt 1 и αe 1 , αt 1 преломления (ввода) отсчитываются от нормали к границе раздела в точке падения (ввода), они связаны между собой и углом падения β через соответствующие скорости законом Снеллиуса (закон «синусов» в оптике» в оптике):
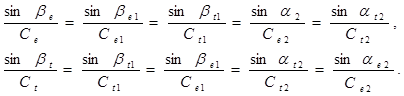(3)
Здесь Ce 1 , Ct 1 скорости продольной и поперечной волн в первой среде;
Ce 2 , Ct 2 – то же, но во второй среде.
Из соотношения Снеллиуса следует: для волны одного типа угол отражения равен углу падения; угол отражения волны другого типа, чем падающая, а также углы преломления волн тем больше, чем выше скорость их распространения.
Частный случай - нормальное падение волны. Это наиболее простая ситуация, так как β=0 и, следовательно, α=0. Отсюда главная особенность – нет явления трансформации волн, отраженная и прошедшая волны будут того же типа, что и падающая.
1) βe =0 – нормальное падение «1» - волны. Тогда
и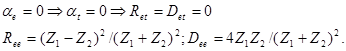 
Данный случай сводится к частному, трансформация отсутствует, выражения для R и D совпадают.
2) Увеличиваем угол падения (Рисунок 6а) до тех пор, когда уже продольная волна не вводится во вторую среду, а «скользит» вдоль границы раздела, т.е. αe =900 . При этом угол падения принимает значение βe = βkp 1. Из (3) при αe =900 получаем, что sin βkp 1 =Ce 1 /Ce 2 . Так Ce 1 /Ce 2 1, то такой угол существует, если βkp 1 =27,50 . Например, для пары «оргстекло-сталь» первый критический угол βkp 1 =27,50
3) Пусть в диапазоне βe > βkp 1 растет βe . Теперь (рисунок 6,б) во вторую среду вводится поперечная волна. При значении βe = βkp 2 уже поперечная волна будет «скользить» вдоль границы двух сред. Из (3) очевидно, что sinβкр2 =Сe 1 /Ct 2 , так как αt =900 , это означает, что βkp 2
существует, когда Ct 2 Ce 1 . Например, для пары «оргстекло-сталь» второй критический угол существует и равен 540 . Заметим, что выполнение условия βkp 1 <β< βkp 2 на практике используется как способ возбуждения поперечных волн. За вторым критическим углом во вторую среду уже ничто не вводится. Вдоль поверхности в этом случае распространяется неоднородная волна. Она самостоятельно не существует, в данном случае она «живет» за счет энергии падающей, является продольной, но на своем пути теряет энергию, переизлучая ее в поперечную (рисунок 4,б), и с глубиной быстро затухает.
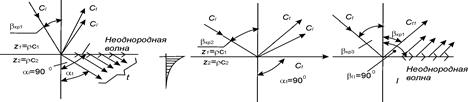
а б в
Рисунок 4 - Отражение и преломление ультразвуковых волн при различных углах падения
1. Поперечная волна падает под углом βt на границу раздела твердой и газообразной сред. Для любого твердого материала (первая среда) существует такой угол βkp 3 , когда отраженная продольная волна будет «скользить» вдоль границы двух сред (рисунок 4,в). Тогда 
, что возможно, так как всегда 
/. При углах, больших βkp 3, эта неоднородная волна существует, но энергию она отдает сразу. Для пары «сталь-воздух» третий критический угол βkp 3 =340 .
Теперь можно проследить, как изменяются коэффициенты отражения Rtt и Rt 1 и коэффициенты прозрачности Dll и Dlt , это иллюстрируется рисунке 5. На рисунке 5, а показана зависимость Dll (β) и Dlt (β) для пары «оргстекло-сталь». В области малых углов βl =(0-100 ) в стали существует практически только продольная волна, что используется при ультразвуковом контроле КП. Далее, вплоть до первого критического угла 
идет область одновременного существования волн двух типов. Эту область в дефектоскопии используют редко. В интервале между первым и вторым критическими углами существует только поперечная волна. Эту область наиболее часто используют в дефектоскопии КП для возбуждения в стали поперечных волн. За вторым критическим углом 
может быть возбуждена поверхностная волна.
а б
Рисунок 5 – Зависимости 
и 
при отражении волны от границы раздела «твердая среда-газ»