Курсовая работа: Уравнение Лапласа, решение задачи Дирихле в круге методом Фурье

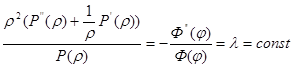
Отсюда получим два обыкновенных дифференциальных уравнения:

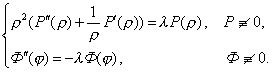
Определим знак :

1 случай. Пусть например

Рассмотрим уравнение (5)

Характеристическое уравнение имеет вид

Это решение не подходит, так как при изменении угла на величину однозначная функция должна вернуться к исходному значению (условие периодичности).

Отсюда следует, что является периодической функцией угла с периодом .

2 случай Пусть , тогда

- это решение подходит для уравнения (5) системы при условии, что А=0.

Рассмотрим уравнение (4) системы:

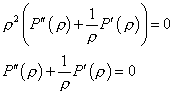
Пусть , тогда:

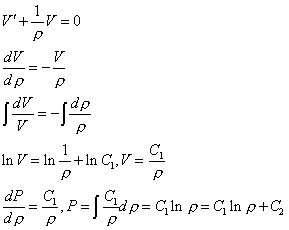
Таким образом, получаем: - решение уравнения в общем случае.

3 случай Пусть .

Решение уравнения (5):

причем q.

Рассмотрим уравнение (4) системы:

Функцию будем искать в виде

Подставим в уравнение (4):