Курсовая работа: Условия неопредел нности критерий Сэвиджа 2
(1.1)
Здесь величину W можно трактовать как максимальный дополнительный выигрыш, который достигается, если в состоянии Vj вместоварианта Ui выбрать другой, оптимальный для этого внешнего состояния, вариант.
Соответствующее критерию Сэвиджа правило выбора следующее: каждый элемент матрицы решений [Wij ] вычитается из наибольшего результата max Wij соответствующего столбца. Разности образуют матрицу остатков. Эта матрица пополняется столбцом наибольших разностей Wir . Выбирается тот вариант, в строке которого стоит наименьшее значение [2].
Пример : Обоснование состава ремонтной бригады.
На предприятии решается вопрос о создании ремонтной бригады. Основываясь на применении критерия Сэвиджа, определить наиболее целесообразное число членов бригады. Исходные данные сведены в таблице (1.1), в ячейках которой занесены доходы при разных вариантах (стратегиях). Под стратегией понимается x -число членов бригады и R - количество станков, требующих ремонта.
Таблица 1.1
| x\R | 40 | 30 | 20 | 10 |
| 5 | 50 | 100 | 180 | 250 |
| 4 | 80 | 70 | 80 | 230 |
| 3 | 210 | 180 | 120 | 210 |
| 2 | 300 | 220 | 190 | 150 |
В этом случае составляется новая матрица, элементы которой составляются по правилу:
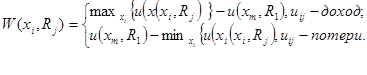 (1.2)
(1.2)
Составим матрицу W(xi , Rj ) - матрицу сожалений для случая, когда uij - потери, используя предыдущие данные. Соответствующая матрица (1.2) получается путем вычисления значений min(xi , Rj ), равных 50, 70, 80 и 150 из столбцов 1, 2, 3, 4, соответственно
Таблица 1.2
| max W(xi , Rj ) | |||||
| 0 | 30 | 100 | 100 | 100 | |
| W(xi ,Rj )= | 30 | 0 | 0 | 0 | 30 |
| 160 | 110 | 40 | 60 | 160 | |
| 250 | 150 | 110 | 0 | 250 |
Таким образом, минимальные потери будут при x=2, когда max W(xi , Rj )=30.
Общие рекомендации по выбору того или иного критерия дать затруднительно. Однако отметим следующее: если определенный риск вполне приемлем, то можно воспользоваться критерием Сэвиджа. [1]
2 Практическая часть.
2.1 Математическая модель задачи.
Исходя из условия задачи, была составлена математическая модель, где была разработана табличная структура задачи табл.(2.1). Определить оптимальный минимальный доход (по критерию Сэвиджа) за день.
Первоначально, случайным образом, в таблицу заносится количество людей, купивших определённый товар в определённый день табл.(2.1).
Таблица 2.1
| Дни | Ассортимент товара | |||
| одежда | обувь | книги | игрушки | |
| День 1 | 1 | 4 | 87 | 21 |
| День 2 | 28 | 68 | 32 | 17 |
| День 3 | 38 | 43 | 9 | 48 |
| День 4 | 8 | 85 | 6 | 30 |
2.2 Аналитическое решение задачи.
Используя таблицу (2.1) и цены на товары
Присвоим табличные данные (2.1) матрице Z. Согласно критерию Сэвиджа Z=min(max(Zij-minZij)), i-день, j-товар, нужно составить новую матрицу, матрицу рисков. Для этого сначала найдём minZ, путём выбора в таблице по столбцам наибольших чисел.
Воспользуясь данными таблицы (2.1) найдём доход за каждый день на каждый товар, с помощью перемножения цены на товар. Цены: одежда - 1, обувь - 2, книги - 3, игрушки - 4. Смотрите таблицу (2.2).
Таблица 2.2
| Дни | Ассортимент товара | |||
| одежда | обувь | книги | игрушки | |
| День 1 | 1 | 8 | 261 | 84 |
| День 2 | 28 | 136 | 96 | 68 |
| День 3 | 38 | 86 | 27 | 192 |
| День 4 | 8 | 170 | 18 | 120 |
Таблица 2.3
| minZ | Ассортимент товара | |||
| одежда | обувь | книги | игрушки | |
| 1 | 8 | 18 | 68 | |
Далее надо найти матрицу, путем вычитания (Zij-minZij), где С1- одежда, С2 – обувь, С3 – книги, С4 - игрушки .
Таблица 2.4
| Дни | Ассортимент товара | |||
| С1 | С2 | С3 | С4 | |
| День 1 | 0 | 0 | 243 | 16 |
| День 2 | 27 | 128 | 78 | 0 |
| День 3 | 37 | 78 | 9 | 124 |
| День 4 | 7 | 162 | 0 | 52 |
Следуя формуле, найдём max(Zij-minZij), выбирая из каждого столбца таблицы (2.4) максимальное число. Отразим это в таблице (2.5).
Таблица 2.5
| max | Ассортимент товара | |||
| одежда | обувь | книги | игрушки | |
| 37 | 162 | 243 | 124 | |
И, наконец, найдём оптимальный минимальный доход, выбрав минимальное число из таблицы (2.5).
Этим числом является 37. Смотрим таблицу (2.5) чтобы найти его расположение. Оно находится в столбце “одежда” и строке “День 3”.