Курсовая работа: Векторный графический редактор

· рисование графических примитивов

· зеркальное преобразование пространства

Алгоритмы рисование графических примитивов

Рисование отрезков прямых

X

????????? ???????? ?????? ???????????? ??? ?????? ??????? LineTo(), ?? ??????? ??????? ?? ?????, ?????????? ??????? ???????, ??? ????????? ?????? ???????. ??????? ??????? ?????????? ? ????????? ?????? ???, ??? ??????????? ?????.

Рисование прямоугольников

Рисование отрезков прямых производится при помощи функции Rectangle(), от текущей позиции до точки, координаты которой указаны, как аргументы данной функции. Текущая позиция изменяется и находится теперь там, где закончилась линия.

X

1)

X

2)

	Y

Рисование треугольников

Рисование треугольников производится при помощи последовательной прорисовки его граней с помощью отдельных линий. Сначала рисуется одна линия, после чего, имея уже две вершины, необходимо задать третью. К точке следующего щелчка курсора из первых 2 вершин прорисовываются еще две линии, все вместе с первой образуя треугольник.

1)

(X0;Y0) – текущая позиция

?

2)

(X1;Y1) – аргументы функций LineTo()

Y

Рисование эллипсов

Для рисования эллипсов нельзя использовать функцию Ellipse(), так как в этом случае пропадает возможность его дальнейшего преобразования «зеркалом». Поэтому рисование эллипсов осуществляется «по точкам», пиксели на форме закрашиваются по заданным математическим формулам, образуя эллипс. При этом визуально создание эллипсов выглядит, как и в случае использования функции Ellipse(): мышью отмечаются координаты верхнего левого и нижнего правого угла прямоугольника, в который вписан эллипс.

X

(ex1;ey1) – текущая позиция

1)

	Y

2)

	Y

Rx=(abs(ex1-ex2))/2;

Ry=(abs(ey1-ey2))/2;

Xc=(ex1+ex2)/2;

Yc=(ey1+ey2)/2;

Алгоритм преобразования пространства

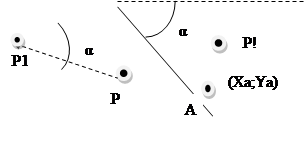
Для преобразования пространства преобразователем типа «зеркало» необходимо начать с создания линии «зеркала». Она рисуется как и обычный примитив line. Далее для зеркального отображения объектов пространства относительно этой линии используется следующий алгоритм состоящий из нескольких шагов:

1.

O

??????? ???????? ?????? ??????? ????? ?? ????? ??????, ???????????? ??????? ?????????????? ??????????????

2. Смещаем преобразуемую точку P пространства на вектор –OB, получаем точку P1

OB

(Xb;Yb)

X

?

	Y

3. Находим угол α между AB и осью ОХ

(Xb;Yb)

OB

X

?

	Y

4. Поворачиваем Р вокруг Р1 на угол α, получаем точку Р2

Р2

X

?

5. Смещаем Р2 на вектор ОВ и получаем точку Р!. Преобразование завершено

Р2

X

?

	Y

4.3 Реализация алгоритма преобразования пространства

Реализацию алгоритма преобразования пространства осуществляет метод Mirror (Листинг 3.1.)