Курсовая работа: Выбор параметров контроля с использованием метода динамического программирования и метода ветвей и границ

xjЄSj=6

H_s (x₆ ) = q1+q2+q3+q4+q5+q7+q8+h₉ ∆с = 0.56334

7) C_s = ∑ c_j ∙x_j , проверяем условие С-С_s . Если с (x_j )> С-С_s , то эти

xjЄS

элементы вводятся в множество E_s .

E_s = {x8,x9,x10}

с₇ =1>b₁ - ∑ c_j ∙x_j =16-1-2-1-4-2-5=1;

xjЄS

с₇ =1£1;

Условие не выполняется.

8) L_s = q1+q2+q3+q4+q5+q6+q7 = 0.61

L_s принимается в качестве приближенного решения L₀ . Так как все вершины дерева, для которых выполняется условие H_s £L₀ , из дальнейшего рассмотрения исключаются, то процесс расчета прекращается.

Таблица 6

№	S	Es	Gs	Hs	xr	Hs(xr)	Hs(xr)	L0
1	Æ	Æ	1…10	0.61	x1	0.61	0.5767
2	x1	Æ	2…10	0.61	x2	0.61	0.5734
3	x1,x2	Æ	3…10	0.61	x3	0.61	0.5967
4	x1,x2,x3	Æ	4…10	0.61	x4	0.61	0.56167
5	x1,x2,x3,x4	Æ	5…10	0.61	x5	0.61	0.5934
6	x1,x2,x3,x4,x5	Æ	6…10	0.61	x6	0.61	0.56334
7	x1,x2,x3,x4,x5,x6	8,9,10	7	0.61	x7	0.61	0.56334
8	x1,x2,x3,x4,x5,x6,x7	8,9,10	Æ	-	-	-	-	0.61

Для контроля системы необходимо использовать следующие параметры контроля: x1,x2,x3,x4,x5,x6,x7.

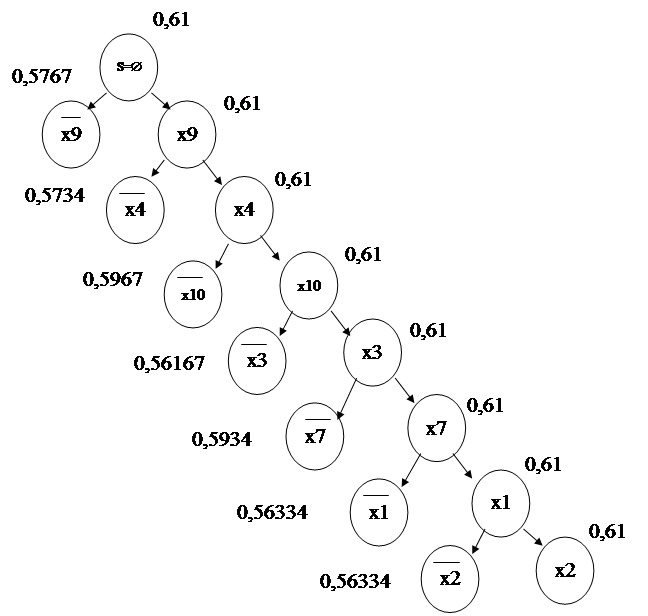
Перейдем на старую нумерацию элементов и построим дерево возможных вариантов решения. Оно представлено на рис.1. Около каждой вершины указана верхняя граница решения. Так как все эти оценки не превышают величины 0,61, то, следовательно, полученное решение L₀ = 0,61 является оптимальным. Таким образом необходимо использовать следующие параметры контроля: x9,x4,x10,x3,x7,x1,x2.

Рис.1

Листинг программы

program vetvi;

const

maxmatrix=1000;

maxsize=200;

type linear=array[1..10000] of integer;

label skip;

var matrix:array[1..1000] of pointer;

n:integer;

sizeofm:word;

q,w,e,r:integer;

start_m:integer;

sm:^linear;

bestx,besty:integer;