Курсовая работа: Вычисление площадей эпюр с использованием численных методов 2
Отделение корней (1-й этап)
Отделить корни уравнения 
, т.е. выяснить сколько корней имеет это уравнение и найти промежутки, в которых они находятся.
Составим таблицу значений и построим график функции 
на промежутке [0.1; 3], с шагом изменения 
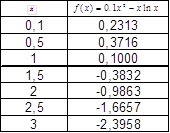
Из таблицы и графика видно, что существует корень уравнения на отрезке [0.5; 1.5]
Уточнение корня (2-й этап)
Метод хорд. Исходя из начального приближения x 0 , удовлетворяющего условию
корень x * уравнения с заданной степенью точности 
вычисляется по формуле
или
В нашем случае условие выполняется для x 0 = a = 0.5. Поэтому итерационный процесс строится по формуле (2)
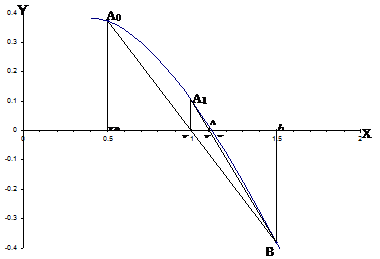
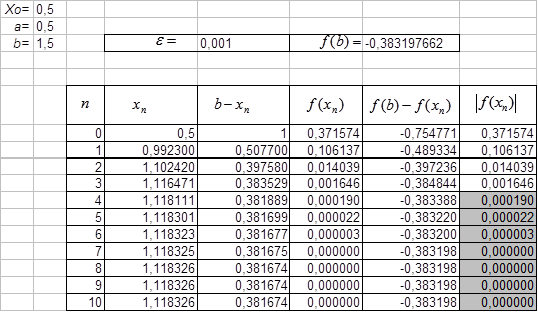
За приближенное решение уравнения по методу хорд с заданной точностью 
принимается 4-я итерация, т.е. x * ≈ 1.1181.
Вывод: Чем выше задается точность - , тем больше итераций.
2. Численное интегрирование (метод входящих прямоугольников)
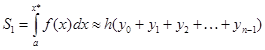
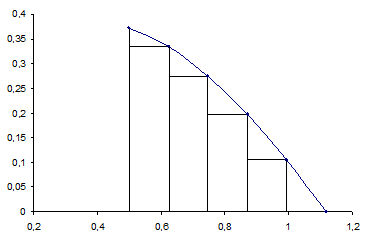
Вычисление площади криволинейной трапеции с разбивкой n =5
На отрезке [a; x* ]; [0.5; 1.1181]
|
Номер шага |
x |
f(x) |
Метод прямоуг. |
|
1 |
0,5 |
0,3716 |
0 |
|
2 |
0,6236 |
--> ЧИТАТЬ ПОЛНОСТЬЮ <-- К-во Просмотров: 276
Бесплатно скачать Курсовая работа: Вычисление площадей эпюр с использованием численных методов 2
|