Курсовая работа: Вычислительная техника и программирование

КУРСОВАЯ РАБОТА

по теме: "Вычислительная техника и программирование"

Киев

Введение

Если задана функция y(x), то это означает, что любому допустимому значению х сопоставлено значение у. Но нередко оказывается, что нахождение этого значения очень трудоёмко. Например, у(х) может быть определено как решение сложной задачи, в которой х играет роль параметра или у(х) измеряется в дорогостоящем эксперименте. При этом можно вычислить небольшую таблицу значений функции, но прямое нахождение функции при большом числе значений аргумента будет практически невозможно. Функция у(х) может участвовать в каких-либо физико-технических или чисто математических расчётах, где её приходится многократно вычислять. В этом случае выгодно заменить функцию у(х) приближённой формулой, то есть подобрать некоторую функцию j(х), которая близка в некотором смысле к у(х) и просто вычисляется. Затем при всех значениях аргумента полагают у(х)"j(х).

Что касается критерия согласия, то классическим критерием согласия является "точное совпадение в узловых точках". Этот критерий имеет преимущество простоты теории и выполнения вычислений, но также неудобство из-за игнорирования шума (погрешности, возникающей при измерении или вычислении значений в узловых точках). Другой относительно хороший критерий — это "наименьшие квадраты". Он означает, что сумма квадратов отклонений в узловых точках должна быть наименьшей возможной или, другими словами, минимизирована. Этот критерий использует ошибочную информацию, чтобы получить некоторое сглаживание шума. Третий критерий связывается с именем Чебышева. Основная идея его состоит в том, чтобы уменьшить максимальное отклонение до минимума. Очевидно, возможны и другие критерии.

Цель задачи о приближении (интерполяции): данную функцию у(х) требуется приблизительно заменить некоторой функцией j(х), свойства которой нам известны так, чтобы отклонение в заданной области было наименьшим. интерполяционные формулы применяются, прежде всего, при замене графически заданной функции аналитической, а также для интерполяции в таблицах.

Один из подходов к задаче интерполяции — метод Лагранжа. Основная идея этого метода состоит в том, чтобы прежде всего найти многочлен, который принимает значение 1 в одной узловой точке и 0 во всех других. Легко видеть, что функция (1) является требуемым многочленом степени n; он равен 1, если X=Xj и 0, когда X=Xi, i¹j.

(1)

Многочлен Lj(x)×Yj принимает значения Yi в i-й узловой точке и равен 0 во всех других узлах. Из этого следует, что (2) есть многочлен степени n, проходящий через n+1 точку (Xi, Yi).

(2)

Другой подход — метод Ньютона (метод разделённых разностей). Этот метод позволяет получить аппроксимирующие значения функции без построения в явном виде аппроксимирующего полинома. В результате получаем формулу для полинома Pn, аппроксимирующую функцию f(x):

P(x)=P(x0)+(x-x0)P(x0,x1)+(x-x0)(x-x1)P(x0,x1,x2)+…+

(x-x0)(x-x1)…(x-xn)P(x0,x1,…,xn);

	разделённая разность 1-го порядка;
	разделённая разность 2-го порядка и т.д.

Значения Pn(x) в узлах совпадают со значениями f(x)

Фактически формулы Лагранжа и Ньютона порождают один и тот же полином, разница только в алгоритме его построения.

Постановка задачи:

1. Построить интерполяционный полином Ньютона по значениям функции в узлах: .

2. Математическая постановка задачи:

Формула выглядит так:

Разделённая разность:

.

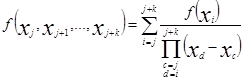1. Алгоритм программы Polinom

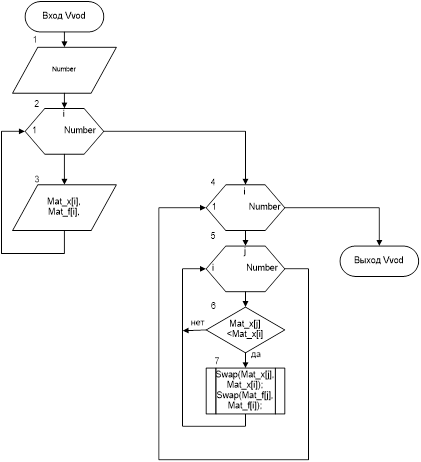
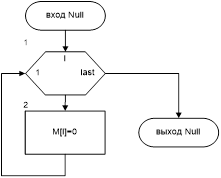
Рис.1Схема алгоритма подпрограммы Swap	Рис.2 Схема алгоритма подпрограммы Null
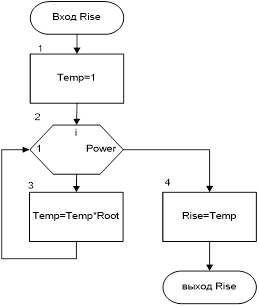
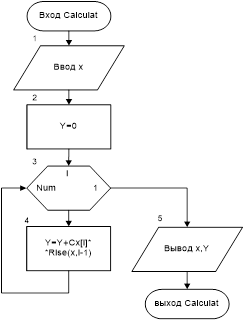
Рис.3 Схема алгоритма подпрограммы Rise	Рис.4 Схема алгоритма подпрограммы Calculat

--> ЧИТАТЬ ПОЛНОСТЬЮ <--