Курсовая работа: Взаимосвязь логистики и маркетинга

Xt-2, …, Xt-n - фактическое значение два периода назад и т.д. до n периодов назад;

w1 – весовой коэффициент, присвоенный спросу прошлого периода (периода (t-1));

w2, …, wn – весовые коэффициенты, присвоенные периодам (t-2) и т.д. до (t-n);

n – количество периодов, учитываемых в прогнозе.

Для вычисления с помощью этого месяца возьмем 4 варианта весовых коэффициентов и, используя значения спроса за прошлые месяцы, сделаем расчет на следующие:

Весовые коэффициенты 1		Весовые коэффициенты 2
Период	Коэффициент	Период	Коэффициент
11 мес. назад	0,3	11 мес. Назад	0,2
12 мес. назад	0,3	12 мес. Назад	0,4
13 мес. назад	0,4	13 мес. Назад	0,4
Весовые коэффициенты 3		Весовые коэффициенты 4
Период	Коэффициент	Период	Коэффициент
11 мес. назад	0,2	11 мес. Назад	0,1
12 мес. назад	0,3	12 мес. Назад	0,4
13 мес. назад	0,5	13 мес. Назад	0,5

Рассчитаем по формуле прогнозные значения потребности в соке на декабрь 2010, январь, февраль, март 2011:

Месяц	Тыс. упаковок
ноя.09	45
дек.09	48
янв.10	40
фев.10	40
мар.10	42
апр.10	41

Месяц	Спрос, тыс. упак.	Вес 1	Откл-е	Вес 2	Откл-е	Вес 3	Откл-е	Вес 4	Откл-е
дек.10	42	41,40	0,60	41,80	0,20	41,70	0,30	42,10	0,10
янв.11	44	41,50	2,50	41,20	2,80	41,60	2,40	41,30	2,70
фев.11	45	41,40	3,60	41,20	3,80	40,90	4,10	40,70	4,30
мар.11	41	43,50	2,50	43,40	2,40	43,20	2,20	43,10	2,10
Среднее отклонение	2,3	2,3	2,25	2,3

Вывод: наименьшее среднее отклонение характерно для прогноза спроса по 3 варианту набора весов (2,25). Это значение больше значения отклонения по прогнозу простой скользящей средней по 6 месяцам (2,08).

2.1.3 Определение потребности на товар методом доверительного интервала

Доверительный интервал – это интервал, в который с заданной вероятностью попадет следующее значение ряда. Этот метод применяется, когда спрос на товар стабилен, не имеет выраженных сезонных колебаний, и у нас есть данные о спросе за достаточно длительный период времени.

Определяем среднее квадратическое отклонение спроса (статистический показатель, показывающий насколько равномерен наш ряд значений. Если значения мало отличаются друг от друга, среднее квадратическое отклонение будет невелико; если наблюдается большой разброс значений, этот показатель будет большим) по формуле:

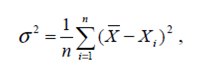
где s – среднее квадратическое отклонение спроса;

X – среднее арифметическое значение спроса;

Хi – значение спроса в каждом периоде;

n – число рассматриваемых периодов.

Рассчитываем величину отклонения от центра интервала (центром

доверительного интервала является среднее арифметическое значение,

рассчитанное в шаге А) по формуле

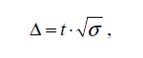
где – величина отклонения от центра интервала;

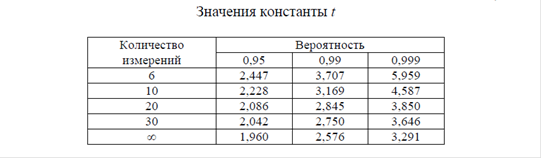
t – коэффициент доверия (некоторые значения приведены в таблице 1).

Спрос на сок «Тонус»:

месяц	Тыс. упаковок
окт.10	43
ноя.10	39
дек.10	42
янв.11	44
фев.11	45
мар.11	41

s² =

s = =1,97

Рассчитываем величину отклонения от центра интервала по формуле:

D=t*

где D - величина отклонения от центра интервала;

t – коэффициент доверия.