Курсовая работа: Задача составления оптимального графика ремонта инструмента

(2.2.22)

Величины {∆_j } равны симплекс-разностям для переменных {x_j } с противоположным знаком. Следовательно, для того чтобы значение целевой функции увеличилось, необходимо выбрать направляющий столбец А_j с наибольшей по модулю отрицательной оценкой, то есть

.

Для решения задачи симплекс-методом на каждой итерации заполняют симплекс-таблицу 2.2.

Таблица 2.2.

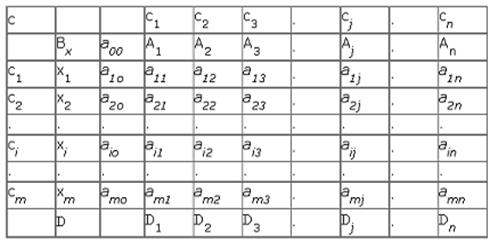
Последняя строка таблицы - индексная служит для определения направляющего столбца. Ее элементы ∆_j определяют по формуле (2.2.21). Очевидно, для всех базисных векторов {A_i } i=1,.,m оценки ∆_i =a_{0 i} =0.

Значение целевой функции a₀₀ определяется из соотношения

.

В столбце B_x записываем базисные переменные {x_i } i= 1, ..., т. Их значения определяются столбиком свободных членов a_i0 , то есть x_i = a_i0 , i=1, 2,.,m.

Направляющие строка A_i и столбец A_j указываются стрелками. Если в качестве направляющего элемента выбран a_ij , то переход от данной симплекс таблицы к следующей определяется соотношениями (2.2.16) - (2.2.18).

Алгоритм решения задачи ЛП табличным симплексом-методом состоит из этапов.

1. Рассчитывают и заполняют начальную симплекс-таблицу с допустимым единичным базисом, включая индексную строку.

2. В качестве направляющего столбца выбирают A_j , для которого .

3. Направляющая строка A_і выбирают из условия

4. Делают один шаг (итерацию) метода полного исключения Гаусса с направляющим элементом a_ij , для чего используют соотношения (2.2.16) - (2.2.18). В частности, элементы индексной строки новой таблицы вычисляют в соответствии с формулой

l=1,2, ..., n.

Правильность вычислений контролируют по формулам непосредственного счета:

(2.2.23)

(2.2.24)

В столбце B_x новой таблицы заменяют x_i на x_j , а в столбце С c_i на c_j .

5. Если все a_0l ^(k+1) ≥0, l=1,.,n, то новое базисное решение x_i = a_i0 ^(k+1) , i € I_б ^(k+1) - оптимально. В противном случае переходят к этапу 2 и выполняют очередную итерацию.

6. Второй, третий и четвертый этапы повторяют до тех пор, пока одна из итераций не закончится одним из двух исходов:

а) все a_0l ≥0. Это признак (критерий) оптимальности базисного решения последней симплекс-таблицы;

б) найдется такой a_0j =∆_j <0, что все элементы этого столбца a_rj ≤0, (r = 1, ., m). Это признак неограниченности целевой функции z = ∑c_j x_j на множестве допустимых решений задачи.

3.2 Метод искусственных переменных

Пусть ограничения задачи ЛП имеют вид A_x ≤A₀ .

Если все b_i ≥ 0, i = 1, 2,..., m, то свободные векторы, образующие единичную подматрицу, составляют базис, а соответствующие им переменные - начальное базисное решение.

В общем случае, когда некоторые ограничения имеют знак «≥», например a_{i 1} x₁ + a_{i 2} x₂ +...+a_in x_n ≥b_i , i=1,2,...., m,