Курсовая работа: Защищенность выборки символов

Кроме того, выборка может быть как непрерывной (т.е. выборка состоит из последовательно стоящих (рядом находящихся) элементов пароля), так и произвольной. То есть выборка - это произвольная последовательность произвольных символов пароля.

2.1 Вероятность входа в систему при фиксированной длине выборки на нижнем и верхнем пределах.

Чтобы рассчитать вероятность входа, вернёмся к классическому определению вероятности. В начале рассчитаем вероятность входа при фиксированной длине на нижнем пределе (длина выборки 3 символа).

Тогда событие «А» - отгадывание злоумышленником элементов выборки из 3 символов и вход в систему. Число случаев, благоприятствующих событию «А» равно 1. Общее число случаев будет равняться. Подставим эти значения в формулу P(A)=m/n и получим:

Теперь рассчитаем вероятность входа при фиксированной длине выборки на верхнем пределе (длина выборки 5 символов).

Тогда событие «В» - отгадывание злоумышленником элементов выборки из 5 символов и вход в систему. Аналогично событию «А», число случаев, благоприятствующих событию «B» равно 1. Общее число случаев будет равняться .

Подставим эти значения в формулу P(B)=m/n и получим:

Если сравнить полученные значения вероятностей, то получим, что вероятность входа при фиксированной длине выборки на нижнем пределе в 3844 раза выше, чем на верхнем пределе.

2.2 Вероятность входа при случайной длине выборки.

Рассмотрим случай, когда система использует случайную длину выборки символов.

Мы уже вычисляли:

P(A) = (выборка 3 символа)

P(B) = (выборка 5 символов).

Теперь вычислим вероятность входа в систему для выборки из 4 символов:

P(C)=(выборка 4 символа).

Для того чтобы определить вероятность входа в систему при случайной длине выборки необходимо ещё знать вероятность выпадения каждой выборки из заданной длины (от 3 до 5 символов). Необходимо учесть, что вероятность выдачи системой любой из выборок от 3 до 5 символов является равновероятна:

= 1/3.

Теперь мы можем вычислить вероятность входа при случайной длине выборки, используя формулу 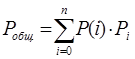, где P(i) – вероятность благоприятного исхода i-го события, P_i – вероятность выпадения i-го события.

Вероятность входа в систему при случайной длине выборки будет равна:

2.3 Сравнение вероятности входа при фиксированной длине выборки со случайной длиной. Оценка эффективности метода случайной выборки символов.

Теперь сравним вероятность отгадывания пароля и входа в систему при случайной длине выборки с вероятностью, которую мы получили при фиксированной длине выборки.

P_{выб 5} () < P_случ. (1,42155*10^-6 ) < P_{выб 3} ()

Вероятность входа при случайной длине выборки всего в несколько раз

(в 2,95 ≈ 3 раза) меньше, чем при фиксированной длине выборки на нижнем пределе; и более чем в 1000 раз больше, чем на верхнем пределе.

Близость вероятности входа при случайной длине выборки и вероятности входа при фиксированной длине выборки на нижнем пределе объясняется следующим:

- распределение вероятностей выдачи системой любой из выборок от 3 до 5 символов является равновероятной;

- вероятность входа в систему при угадывании выборки в 3 символа на несколько порядков (в 62 и в 62² раза) больше остальных.

Следовательно вероятности входа при угадывании выборок в 4 и 5 символов незначительно влияют на общую вероятность.

Полученные числовые данные показывают, что метод случайной выборки символов эффективнее в плане несанкционированного входа, чем метод использования фиксированной длины выборки.