Курсовая работа: Зеркальные антенны

причем

Учитывая это и интегрируя d Е_m по раскрыву, имеем следующее выражение для электрического поля дальней зоны антенны в плос­кости α = 0:

Для получения простого результата идеализируем задачу, взяв q_m (r ', α') = e₀ const, т. е., в сущности, приняв раскрыв зеркала за идеальную поверхностную антенну в форме круга. Тогда

Принимая во внимание, что интегрирование по α' приводит к функции Бесселя нулевого порядка, которая имеет интегральное представление

пишем

а интегрирование по r' дает

Из этого выражения нетрудно получить нормированную харак­теристику направленности зеркала в меридиональной плоскости учитывая, что

В результате

Далее, нетрудно найти угловую ширину главного максимума излучения по нулям. Первый корень уравнения J₁ (x) = 0 равен В₁₁ = 3,832.

Полагая sin υ₀ ≈ υ_0, имеем

Полученные формулы оказываются бо­лее достоверными для длиннофокусных зер­кал, облучаемых обычно равномернее, чем короткофокусные.

Учет действительных характеристик на­правленности реальных облучателей требует уже весьма громоздких математических действий, которые не приводятся. Остановимся лишь на некоторых результатах, обычно ис­пользуемых при расчете зеркальных антенн.

Подробнее других изучено параболическое зеркало, облучаемое элементарным электрическим вибратором, снабженным плоским контррефлектором (рис.8). Характеристика направленности в меридиональной плоскости при этом выражается формулой

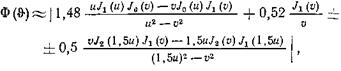Где

Знак плюс берется в том случае, когда меридиональная плоскость проходит через облучающий вибратор (плоскость Е), а минус — в случае перпендикулярной вибратору меридиональной плоскости (плоскость Н).

Кнд антенны в которой коэффициент использования раскрыва x равен:

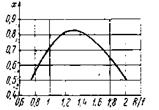
График функции х(R/f) показыва­ет, что найвыгоднейшим при данном типе облучателя является отношение радиуса зеркала к фокусному расстоянию:

при котором

Существование оптимума объясняется следующим образом: при удалении облучателя кнд антенны должен был бы возрастать в результате повышения равномерности облучения, однако при этом уменьшается угол, под которым видно зеркало (рис.8а), так что увеличивается доля энергии, уходящей за его край, что снижает кнд.

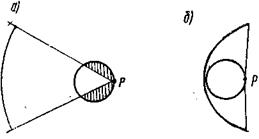
Рис.8

Короткофокусное зеркало (рис.8б) облучается почти без потерь, но неравномерно. Можно убедиться, что максимальный коэффициент использования соответствует состоянию, при котором амплитуда поля дипольного облучателя на краю зеркала составляет около 1/3 максимальной.

На рис.9а, б показано распределение тока в зеркале при дипольном облучателе. Ток, наводимый на короткофокусном зерка­ле (рис.9б), собирается у двух полюсов, расположение которых нетрудно определить из рис.9в: они лежат на пересечениях оси облучателя с поверхностью параболоида.

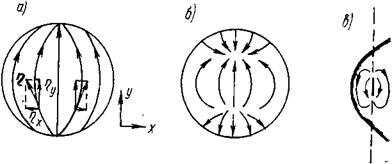
Рис. 9

В результате существова­ния полюсов часть зеркала несет противофазный ток, уменьшающий излучение в осевом направлении. Как говорят, зеркало имеет при этом «вредные зоны». Однако и в тех случаях, когда вредных зон нет, нельзя игнорировать специфического искривления линий тока в результате неоднородности поля облучателя.

4. Применение параболических зеркал в антенной технике