Курсовая работа: Знаходження оберненої матриці за формулою

2. Знайти матрицю, обернену до матриці.

A =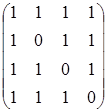

Знаходимо спочатку визначник матриці A:

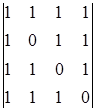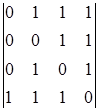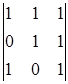= = 1(-1)⁴⁺¹ 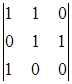= (-1) =

= (-1)1(-1)³⁺¹ = -1 0. Отже обернена матриця існує.

Знаходимо алгебраїчні доповнення:

A₁₁ =(-1)¹⁺¹ 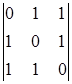= 2 A₂₁ =(-1)²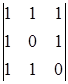⁺¹ = -1

A₃₁ =(-1)³⁺¹ 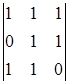= -1 A₄₁ =(-1)⁴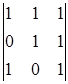⁺¹ = -1

A₁₂ =(-1)¹⁺² 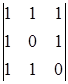= -1 A₂₂ =(-1)²⁺² 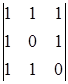= 1

A₃₂ =(-1)³⁺² 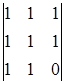= 0 A₄₂ =(-1)⁴⁺² 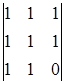= 0

A₁₃ =(-1)¹⁺³ 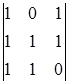= -1 A₂₃ =(-1)²⁺³ 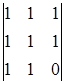= 0

A₃₃ =(-1)³⁺³ 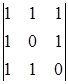= 1 A₄₃ =(-1)⁴⁺³ 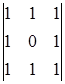= 0

A₁₄ =(-1)¹⁺⁴ 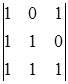= -1 A₂₄ =(-1)²⁺⁴ 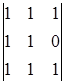= 0

A₃₄ =(-1)³⁺⁴ 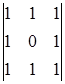= 0 A₄₄ =(-1)⁴⁺⁴ 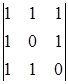= 1

Підставляючи у формулу (3) знайдені значення, одержуємо:

A^-1 =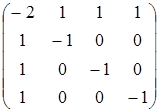

Перевірка. Одержаний результат можна легко перевірити.

Оскільки, AA^-1 = E, де E –це одинична матриця, то:

AA^-1 = =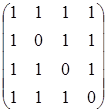

=

=

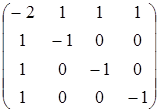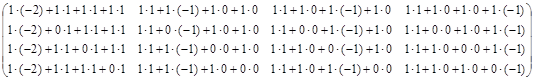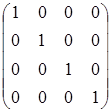
Отже, обернену матрицю знайдено вірно.

Висновки

Отже, висвітливши основні поняття обернених матриць, можна прийти до висновку, що процес знаходження обернених матриць за допомогою формули є швидким і простим методом аналізу стану певного об’єкта.

Список використаної літератури

1. Ващук Ф.Г., Поляк С.С. Практикум з вищої математики. - Ужгород, 2005. 6 – 24 с.

2. Курош А.Г. Курс высшей алгебры. - Москва, 1968. 95–99 с.

Додаток

Дану задачу можна реалізувати на мові програмування Turbo Pascal

Лістінг програми

Program InversMatrix;

const max_size=10; {max size matrix }

type matr=array[1..max_size,1..max_size] of real;