Лабораторная работа: Динамические структуры данных

и тогда можно выполнять присваивание: Е2. dlink: = E1.

Бинарные деревья

Деревья относятся к разряду структур, которые удобно строить в динамической памяти с использованием указателей. Наиболее важный тип деревьев - двоичные (бинарные) деревья, в которых каждый узел имеет самое большее два поддерева: левое и правое. Подробнее, если имеем дерево вида (рис.1a), то ему может соответствовать в динамической памяти структура (рис.1б).

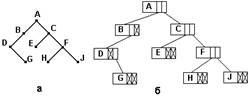
Рис.1. Двоичное дерево и его представление с помощью списочных структур памяти а - двоичное дерево; б - представление дерева с помощью списков с использованием звеньев одинакового размера

Для построения такого бинарного дерева используется следующий ссылочный тип:

Type Ptr=Node Node=record Info=Char Llink,Rlink=Ptr End

Для работы с деревьями имеется множество алгоритмов. К наиболее важным относятся задачи построения и обхода деревьев. Пусть в программе дано описание переменных:

var t: ptr; s: integer; c: char; b: boolean;

Тогда двоичное дерево можно построить с помощью следующей рекурсивной процедуры:

procedure V (var t: ptr) var st: string begin readln (st) if st<>'. 'then begin new (t) t. info: =st V (t. Llink) V (t. Rlink) end else t: =nil end

Структура дерева отражается во входном потоке данных: каждой вводимой пустой связи соответствует условный символ (в данном случае точка). Для примера на рис.1 входной поток имеет вид:

A B D. G... C E. F H. J...

Существует три основных способа обхода деревьев [1]: в прямом порядке, обратном и концевом. Обход дерева может быть выполнен рекурсивной процедурой и процедурой без рекурсии (стековый обход). В приведенной ниже рекурсивной процедуре выполняется обход дерева в обратном порядке.

Рrocedure PR (t: ptr) {рекурсивный обход дерева} begin if t<>nil then begin PR (t. Llink) {обойти левое поддерево} writeln (t. info) {попасть в корень} PR (t. Rlink) {обойти правое поддерево} end end

Нерекурсивный алгоритм обхода дерева в прямом порядке:

Пусть T - указатель на бинарное дерево; А - стек, в который заносятся адреса еще не пройденных вершин; TOP - вершина стека; P - рабочая переменная.

1. Начальная установка: TOP: =0; P: =T.

2. Если P=nil , то перейти на 4. {конец ветви}

3. Вывести P. info. Вершину заносим в стек: TOP: =TOP+1; A [TOP]: =P; шаг по левой ветви: P: =P. llink ; перейти на 2.

4. Если TOP=0 , то КОНЕЦ .

5. Достаем вершину из стека: P: =A [TOP]; TOP: =TOP-1 ;

Шаг по правой связи: P: =P. rlink; перейти на 2.

2. Условия задачи

17.16. Деревом поиска, или таблицей в виде дерева, называется двоичное дерево в котором слева от любой вершины находятся вершины с элементами, меньшими элемента из этой вершины, а справа - с большими элементами (предполагается, что все элементы дерева попарно различны и что их тип (ТЭД) допускает применение операций сравнения); пример такого дерева показан на рис.21.

Считая описанными тип дерево ( см. выше) и тип файл type файл=file of ТЭД; определить функцию или процедуру, которая:

а) проверяет, входит ли элемент Е в дерево поиска Т;

б) записывает в файл f элементы дерева поиска Т в порядке их возрастания;

в) добавляет к дереву поиска Т новый элемент Е, если его не было в T ;