Лабораторная работа: Дослідження трифазної системи при з’єднанні споживачів трикутником

Вивчити основні властивості і застосування трифазних кіл при з’єднанні джерела і споживачів трикутником. Дослідити режими роботи трифазних кіл при рівномірному і нерівномірному навантаженні фаз, а також при обриві фази або одного із лінійних проводів. Навчитися розраховувати трифазні кола при навантаженні фаз активними опорами.

9.2 Короткі теоретичні відомості

???? ??????? ?????????? ?????????? (??????????????) 璺????? ??? ????? ???, ??? ?????? ?????? ??? 璺?????? ? ???????? ??????, ?????? ?????? ? ???????? ???????, ? ?????? ??????? ? ???????? ?????? ? ?? ????? 璺????? ?????????? ??????? ???????, ?? ???????? 璺?????? ??????????? (???. 9.1). ??????????? 璺???????? ? ?????????. ? ?????????? ??????? ??????? ?????????? ??? ??????????? ???????????? (????? ????????? ????) ????? ????????? ?? ????, ?? ???? ???????? ??????? ?.?.?. ???? ??????????? ????, ???????? ???? ?????? ????? ?? ??????????, ??? ??????? ?? ????? ?? ??? .

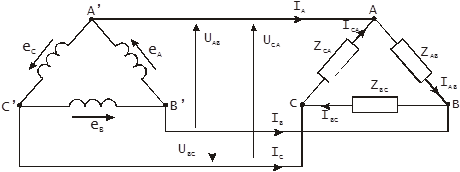
Рис.9.1

В схемі, наведеній на рис.9.1, трикутник повних опорів з’єднаний з трикутником фазних обмоток генератора (трансформатора) лінійними проводами.

Напруги між лінійними проводами дорівнюютьнапругам між початком і кінцем кожної фази,тобто

. /9.1/

Лінійні струми ІA, ІB, ІC не дорівнюють фазним струмам. Співвідношення між ними можна знайти на підставі першого закону Кірхгофа, згідно з яким сума миттєвих значень струмів в будь-якому вузлі (розгалуженні) електричного кола дорівнює нулю. Згідно з цим законом запишемо, що

/9.2/

Із рівнянь /9.2/ видно, що лінійні струми дорівнюють різниці суміжних фазних струмів:

/9.3/

Замінивши в рівняннях /9.3/ миттєві значення струмів векторами, одержимо:

/9.4/

На підставі рівнянь /9.4/ можна побудувати векторну діаграму струмів і знайти співвідношення між лінійними і фазними струмами. На рис.9.2 побудована векторна діаграма для випадку і

Фазні струми визначали за законом Ома:і .

а). б).

Рис.9.2

Із трикутника струмів ВКМ знаходимо

Отже, при з’єднанні симетричного споживача трикутником лінійні струми більші за фазні у разів. Якщо система несиметрична, то фазні струми будуть різними, різними будуть і кути зсуву фаз, але методика побудови векторної діаграми і визначення лінійних струмів залишається такою ж самою.

На рис.9.2, б побудована векторна діаграма при нерівномірному навантаженні фаз активними опорами, що характерне при живленні освітлення лампами розжарювання житлових будинків.

Граничним випадком нерівномірного навантаження фаз є збільшення опору фази до безмежності (), що відповідає режиму обриву фази у місці з’єднання з лінійним проводом. У цьому випадку струму в обірваній фазі, наприклад, у фазі АВ, не буде (IAB=0). Струми в інших фазах не зміняться, бо не змінились фазні напруги. Проте лінійні струми IA і IB згідно з рівнянням /9.4/ зменшаться і стануть рівними відповідним фазним: IA=ICA і IB=IBC. Лінійний струм IC=ICA – IBCне зміниться.

?? ???. 9.3, ? ?????????? ???????? ???????? ?????? ? ??????? ??? ????????? ???????????? ? ?????? ???? ??, ??? ?????????? ????????? /9.4/ ?? ????? IAB=0.

Якщо до обриву фази АВ добавити ще обрив фази ВС, то трифазна система перетвориться в однофазну і струм буде протікати тільки в фазі СА. Лінійні струми IA і IC будуть рівні за величиною і протилежні за напрямком, як витікає з рівнянь /9.4/ при підстановці IAB=IBC =0. Векторна діаграма для цього випадку побудована на рис. 9.3, б.

Окрім обриву фаз, може виникнути і обрив лінійного провода. У цьому випадку нормальний режим збережеться у фазі ВС, якщо обірвано лінійний провід А. Дві інші фази будуть з’єднані послідовно і до них буде прикладена повна лінійна напруга. Тому падіння напруг в них розподілиться пропорційно опорам фаз.

На рис.9.3,в наведені діаграми напруг.і струмів при різних активних опорах фаз і обриві лінійного провода А. Як слідує із рис. 9.3,в у цьому випадку

--> ЧИТАТЬ ПОЛНОСТЬЮ <--