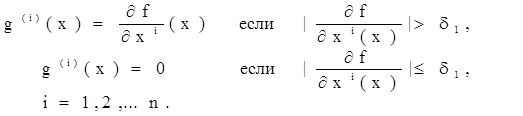Лабораторная работа: Градієнтні методи
хк+1 = хк - aдо ![]() ,
, ![]()
де aдо - мінімум задачі одномірної мінімізації:
Крок 3.
Обчислюється значення градієнта в точці хк+1 : ![]() .
.
Крок 4.
Якщо ||![]() ||£e3 , то пошук точки мінімуму закінчується й покладається:
||£e3 , то пошук точки мінімуму закінчується й покладається:
![]()
Інакше до=до+1 і перехід до кроку 2.
1.5 Методи ярів
1.5.1 Загальна характеристика
Градієнтні методи повільно сходяться в тих випадках, коли поверхні рівня цільової функції f (x) сильно витягнуті. Цей факт відомий у літературі як "ефект ярів". Суть ефекту в тім, що невеликі зміни один змінних приводять до різкої зміни значень функції - ця група змінних характеризує "схил яру", а по іншим змінним, що задає напрямок "дно яру", функція міняється незначно. На малюнку зображені лінії рівня "яружної" функції траєкторія градієнтного методу характеризується досить швидким спуском на "дно яру", і потім повільним зиґзаґоподібним рухом у точку мінімуму.
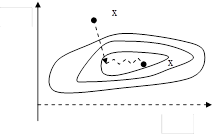
Існують різні підходи для визначення точки мінімуму функції f (x) у яружній ситуації. Більшість із них засновані на евристичні (тобто інтуїтивних, не обґрунтованих строго) міркуваннях. Їх можна застосовувати в ситуаціях, коли застосування більше зроблених методів неможливо або недоцільно, наприклад, значення цільової функції обчислюється зі значними погрішностями, інформація про її властивості недостатня, і т.д. Ці методи прості в реалізації й досить часто застосовуються на практиці, дозволяючи в ряді випадків одержати задовільне рішення задачі.
Схема яружного методу 1.
Евристичні алгоритми
Іноді, використовуючи градієнтний спуск для мінімізації функцій зі складною топографічною структурою, застосовують евристичні схеми, які ідейно близькі до методів спуска. Ми розглянемо дві такі схеми.
Перша евристична схема містить два основних етапи. Обидва етапи являють собою аналоги градієнтного спуска з постійним кроком. Тільки замість градієнта ![]() використовується вектор g (x), формований з координат
використовується вектор g (x), формований з координат ![]() , але на кожному з етапів за різними правилами.
, але на кожному з етапів за різними правилами.
На першому етапі задається мале число d1 <<1 і використовується градієнтний спуск, де замість градієнта ![]() береться вектор g (x) ={g (1) ( x),…,g (n) ( x) }, який визначається в такий спосіб:
береться вектор g (x) ={g (1) ( x),…,g (n) ( x) }, який визначається в такий спосіб:
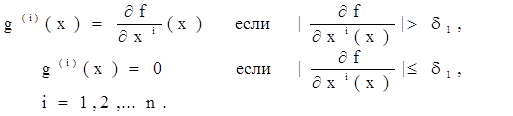
![]()
Таким чином, спуск виробляється лише по тими змінним, у напрямку яких похідна цільової функції досить велика. Це дозволяє швидко спуститися на "дно яру". Ми спускаємося доти, поки метод не зациклиться, тобто доти, поки кожна наступна ітерація дозволяє знайти точку, у якій значення функції менше, ніж значення, знайдене в попередній ітерації. Після цього переходимо до наступного етапу.
На другому етапі задається деяке велике число d2 >>1 і використовується процедура спуска, де замість градієнта ![]() береться вектор g (x) ={g (1) ( x),…,g (n) ( x) }, який визначається в такий спосіб:
береться вектор g (x) ={g (1) ( x),…,g (n) ( x) }, який визначається в такий спосіб:
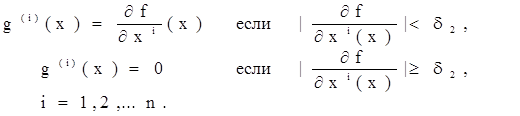
![]()
У цьому випадку переміщення відбувається по "березі" яру уздовж його "дна". Як і на першому етапі, спуск триває доти, поки метод не зациклиться.
Після виконання першого й другого етапів приймається рішення про завершення роботи або продовження. Для цього рівняється норма різниці попередньої точки, тобто точки, що ми мали до застосування першого й другого етапів, з поточною точкою, тобто отриманої після застосування з точністю рішення задачі e1 . Якщо ця норма менше e1 і норма градієнта в поточній точці менше e3 , то пошук закінчується й остання обчислена точка приймається за наближене рішення задачі. Інакше для поточної точки знову повторюємо перший і другий етапи й т.д.
Схема алгоритму
Крок 1.
Задаються х0 , e1 , e3 ,d1 ,d2 ,a1 - постійний крок пункту 1 і a2 - постійний крок пункту 2 (a1 <a2 ). Привласнюється до=0.
Крок 2. (Перший етап).
Із точки хк здійснюється спуск на "дно яру" з постійним кроком a1 .
При спуску обчислення чергової точки здійснюється з використанням формул:
xj+1 = xj - a1 g (xj ), де g (x) ={g (1) ( x),…,g (n) ( x) },