Крок 3. (Другий етап).

Із точки x_l здійснюється спуск уздовж "дна яру" з постійним кроком a₂ . При спуску використовуються формули: x_j+1 = x_j - a₂ g (x_j ), де

g (x) ={g ^{(1) (} x),…,g ^{(n) (} x) },

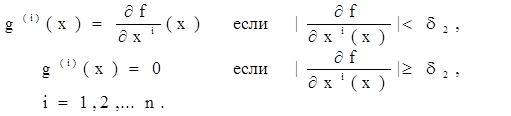
Нехай цей процес зупинився в точці x_m .

Крок 4.

Якщо ||x_k - x_m || £e₁ і || || £e₃ , то думаємо:

і пошук мінімуму закінчується.

Інакше k=m і переходимо до кроку 2.

2. Завдання на лабораторну роботу

1) Вивчити викладені методи багатомірної безумовної оптимізації.

2) У відповідність із варіантом завдання, вказаним викладачем, скласти програми для методів багатомірної безумовної мінімізації й знайти точку мінімуму цільової функції f (x) =f (x ^(1), x ⁽²⁾⁾ із заданою точністю ε зазначеними методами. Початкове наближення x₀ і точність e приводяться в умові задачі. Порівняти результати, отримані різними методами для однієї й тієї ж цільової функції (зокрема, порівняти число обчислень цільової функції і її похідних, що знадобилися для одержання заданої точності). Для кожного використаного методу побудувати траєкторію проміжних точок, які одержані на чергових кроках методу й збіжних до точки мінімуму.

3) Оформити звіт про виконання завдання із приведенням умови задачі, алгоритмів і програм, зазначених у завданні методів мінімізації, графіків траєкторій проміжних наближень, таблиці результатів порівняння розглянутих методів, висновку за результатами порівняння методів.

Методи

1) метод найшвидшого спуску;

2) евристичний алгоритм;

Варіанти завдань

Цільова функція f (x) =f (x ^(1), x ⁽²⁾⁾ залежить від двох аргументів. Функція f (x) наступного виду:

f (x) =a*x ⁽¹⁾ +b*x ⁽²⁾ +e^{c* (x) +d* (x).}

№ вар	№ методу	Цільова функція				Початкове наближення	Точність розв’язку
a	b	c	d
6	3, 6	3	-1,2	0,02	1,3	(-1; 0)	0,0001

Програма до методу № 1

#include <stdio.h>

#include <math.h>

#include <iostream.h>

#include <conio.h>

// ing namespace std;

double f (double x1, double x2)