Лабораторная работа: Исследование нелинейных цепей постоянного тока

ВВЕДЕНИЕ

ЦЕЛЬ РАБОТЫ: Экспериментально определить и построить вольтамперные характеристики нелинейных резистивных элементов; проверить достоверность графического метода расчёта нелинейных электрических цепей.

ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ

Зависимость тока, протекающего через резистивный элемент электрической цепи от напряжения, приложенного к его выходным зажимам, называется вольтамперной характеристикой (ВАХ):

Иногда такой зависимостью служит:

Если график ВАХ является прямой линией, то такой элемент называется линейным элементом (рис. 1).

На примере рис. 1 можно графически представить сущность понятия о линейном элементе. Какое бы напряжение ни было приложено к его выходным зажимам ( и ) ток всегда будет таким ( или соответственно), что отношение

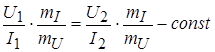
есть постоянная величина, не зависящая от и ( и – масштабы осей напряжения и тока). Учитывая, что для такого резистивного элемента справедлив закон Ома:

Получим:

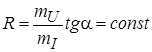
То есть для линейного резистивного элемента его параметр (сопротивление) не зависит от режима работы электрической цепи, в которую он включён.

Если ВАХ не является прямой линией, то такой резистивный элемент будет нелинейным резистивным элементом (рис. 2). Нелинейность зависимости связана с тем, что при изменении ( и ) и ( и соответственно) изменяется их отношение.

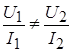или

Т.е. сопротивление нелинейного резистивного элемента не является постоянной величиной и изменяется с изменением и .

В общем случае нелинейный элемент нельзя характеризовать каким-либо постоянным сопротивлением и его характеристикой служит ВАХ, задаваемая таблично, графически (рис. 2) или аналитически.

По аналогии с резистивным элементом можно упомянуть о линейных и нелинейных индуктивном (рис. 3) и ёмкостном (рис. 4) элементах электрических схем, в зависимости от того зависят или не зависят их параметры (индуктивность) и (ёмкость) от режима работы элементов.

Разнообразные электронные, ионные, полупроводниковые и магнитные приборы, нашедшие широкое применение в радиотехнике, автоматике, связи, электротехнике обладают свойствами нелинейных элементов. Это вынуждает разрабатывать методы расчёта нелинейных цепей. Цепь является нелинейной, если один или несколько элементов этой цепи нелинейные.

К нелинейным электрическим цепям применимы основные законы электрических цепей, т. е. общий закон Ома и законы Кирхгофа (для цепей переменного тока эти законы справедливы только в мгновенной форме записи). В тоже время расчёт нелинейных электрических цепей значительно труднее, чем линейных цепей. Объясняется это тем, что кроме токов и напряжений, подлежащих обычно определению, неизвестными являются зависящие от них сопротивления нелинейных элементов.

Для расчёта нелинейных электрических цепей применяются различные методы расчёта: аналитические, графо – аналитические, графические, которые выбираются в зависимости от способа представления ВАХ, сложности схемы, формы питающего напряжения. Наибольшее распространение получил метод линеаризации ВАХ элементов. Сущность метода сводится к замене нелинейного элемента линейным, имеющим постоянное сопротивление. Преобразуя таким образом все нелинейные элементы, нелинейную цепь сводят к линейной. Последнюю рассчитывают известными методами.

В самом простейшем случае (рис. 5), если , то напряжение на зажимах нелинейного элемента и ток, протекающий через, него также будут постоянными. В этом случае нелинейный элемент можно заменить линейным элементом (рис. 6) с сопротивлением - статическое сопротивление нелинейного элемента в точке его ВАХ (рис. 7), определяемое, как отношение напряжения на элементе к току через него:

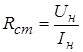
Статическое сопротивление можно определить и графически: как тангенс угла между прямой, проведённой из начала координат через точку на ВАХ и осью токов (рис. 7):

Точка на ВАХ, одновременно отвечающая значениям напряжения и на нелинейном элементе, называется рабочей точкой.

--> ЧИТАТЬ ПОЛНОСТЬЮ <--