Лабораторная работа: Исследование свойств звена при охвате обратной связью
Если задана передаточная Функция W(S), то путём подставки S=jw получаем частотную передаточную функцию W(jw), которая является комплексным выражением т.е.
,
А(w) – вещественная составляющая
К(w) – мнимая составляющая.
Частотная передаточная функция может быть представлена в показательной форме:
где 
– модуль;
– аргумент частотной передаточной функции.
Функция М(w), представленная при изменении частоты от 0 до ¥ получило название амплитудной частотной характеристики (АЧХ).
Функция j(w), представленная при изменении частоты от 0 до ¥ называется фазовой частотной характеристикой (ФЧХ). Для анализа поведения системы в большом диапазоне частот удобно в качестве аргумента частотных характеристик рассматривать не частоту ω, а ее десятичный логарифм ω 10 log.
Порядок выполнения работы
Интегрирующее звено
– дифференциальное уравнение:
– переходная функция:
– передаточная функция: 
Обратная связь интегратора
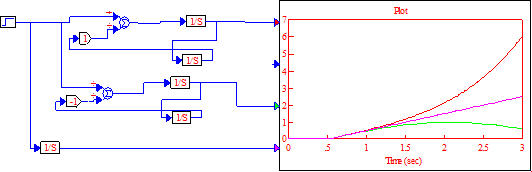
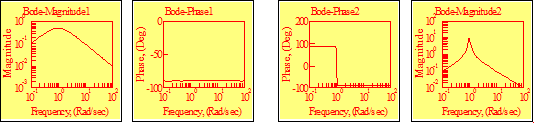
Апериодическое звено
– дифференциальное уравнение:T 
+ y = k u
– переходная функция: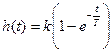 
– передаточная функция: 
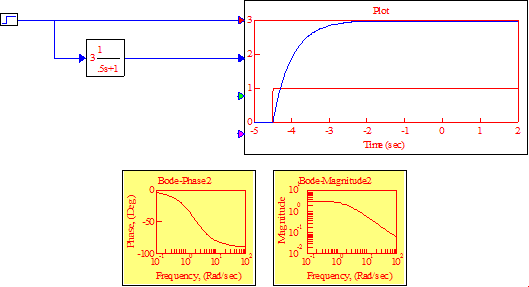
Обратная связь апериодического звена
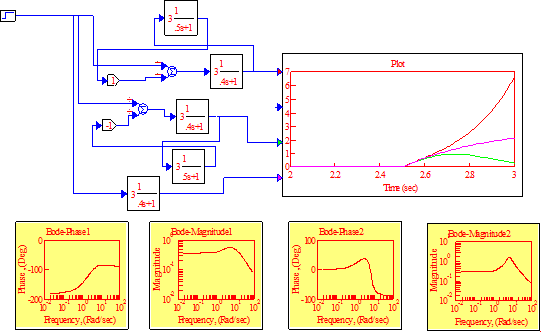
Колебательное звено
– дифференциальное уравнение: T 2 
+ 2 d T
+ y = k u