Лабораторная работа: Исследование цепи переменного тока

Цель работы:

Изучение явления резонанса в цепи переменного тока. Проверка закона Ома для цепи переменного тока.

Оборудование: стенд для исследования явлений в цепи переменного тока, генератор переменного тока ГЗ –109 (генератор звуковой), вырабатывающий переменный ток с частотой 20 – 20 000 Гц, т. е. в «звуковом» интервале частот, магазин сопротивлений, мультиметр.

Незатухающие вынужденные электрические колебания обычно называют переменным током. Частота переменного тока f – это число колебаний в 1 секунду. Частота 50 Гц принята для промышленного тока во многих странах мира. С помощью генераторов переменного тока можно получать переменный ток любой частоты. При этом напряжение на выходе генератора обычно меняется по гармоническому закону

, (1)

где w =2 p f - циклическая частота, f - линейная частота, U_m – амплитуда (максимальное значение) напряжения.

Если источник переменного напряжения (генератор) с частотой w подключить к электрической цепи, то в ней возникнут колебания силы тока той же частоты. Но колебания силы тока не обязательно должны совпадать по фазе с колебаниями напряжения. В общем случае мгновенное значение силы тока i определяется по формуле

, (2)

где j - разность (сдвиг) фаз между колебаниями тока и напряжения, I_m – амплитуда силы тока.

· В проводнике с активным сопротивлением (резисторе) колебания силы тока по фазе совпадают с колебаниями напряжения, а амплитуда силы тока определяется равенством:

, (3)

где R – (активное) сопротивление резистора.

· В катушке индуктивности колебания силы тока отстают от колебаний напряжения на угол j = p /2 . Амплитуда силы тока в катушке равна

.

Величину X_L = w L = 2 p fL (4)

называют индуктивным сопротивлением .

· На конденсаторе колебания силы тока опережают колебания напряжение на угол j = p /2. Амплитуда силы тока равна:

.

Величину (5)

называют емкостным сопротивлением .

Рассмотрим электрическую цепь (рис. 1), состоящий из соединенных последовательно резистора R , конденсатора С и катушки индуктивности L . Эта цепь является колебательным контуром, в которой возможны собственные электрические колебания с частотой

(6)

Если к концам этой цепи приложено переменное напряжение, изменяющееся по закону (1), то в ней возникнут вынужденные электрические колебания с частотой w . Сила этого переменного тока будет определяться по формуле (2), причем для нахождения амплитуды и фазы тока необходимо учесть влияние всех элементов цепи: R , L , С . Лучше всего это можно сделать с помощью векторной диаграммы (треугольника сопротивлений) (рис. 2). Из рисунка видно, что полное сопротивление цепи равно:

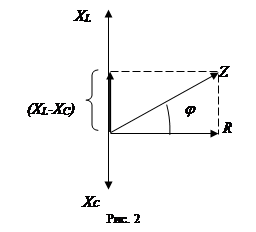
, (7)

а сдвиг фаз между током и напряжением

. (8)

Разность X = ( X_L - X_C ) называется реактивным сопротивлением цепи.

Соотношение

(9)

называют законом Ома для цепи переменного тока (по аналогии с законом Ома для постоянного тока I = U / R ).

Обычные электроизмерительные приборы для переменного тока позволяют измерять эффективные (действующие ) значения силы тока и напряжения, которые связаны с амплитудными значениями:

. (10)

Очевидно, что вид закона Ома для цепи переменного тока не меняется, если вместо амплитудных использовать эффективные значения силы тока и напряжения.

Как известно, резкое увеличение амплитуды колебаний колебательной системы при совпадении частоты вынуждающих колебаний с частотой собственных колебаний системы называется резонансом .

Сила тока в рассматриваемой цепи зависит как от величин R , L , C , так и от частоты w вынуждающих колебаний. Если менять частоту переменного тока, подводимого к рассматриваемой цепи, то при определенной частоте индуктивное сопротивление X_L становится равным емкостному сопротивлению X_C

(11)

При этом полное сопротивление цепи становится минимальным и равным активному сопротивлению цепи Z = R . Сила тока достигает максимального значения - наступает резонанс, причем резонансная частота совпадает с частотой собственных колебаний контура

(12)

При последовательном соединении элементом цепи (как в данном случае) при резонансе падение напряжения на конденсаторе и катушке индуктивности становятся одинаковыми по величине – резонанс напряжений

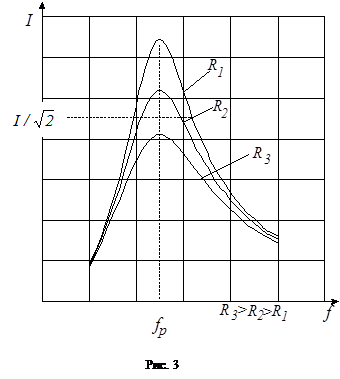
, (13)

причем их величины могут значительно превышать приложенное напряжение.

«Острота» резонансной кривой характеризуется ее относительной полушириной :

, (14)

где D f =( f ₂ – f ₁ ) ) – разность значений частоты, соответствующих . Эта величина Q называется еще добротностью колебательного контура (колебательной системы). Можно показать, что добротность колебательного контура определяется его параметрами:

(15)

Добротность показывает, во сколько раз падение напряжения на конденсаторе и катушке при резонансе больше, чем приложенное напряжение

(16)

--> ЧИТАТЬ ПОЛНОСТЬЮ <--