Лабораторная работа: Корреляционно-регрессионный анализ

Уравнение регрессии между у и х2(степенная):

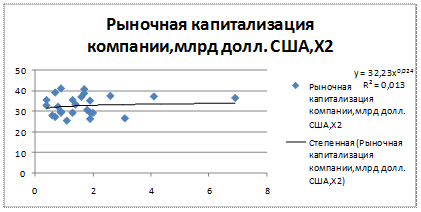
E1	2171
E2	166
E3	165

С помощью пакета анализа

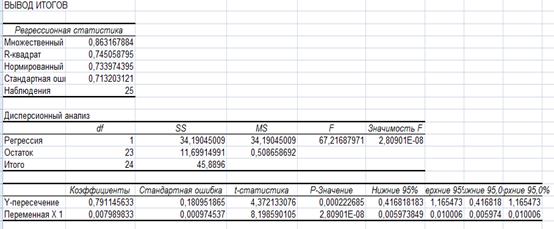
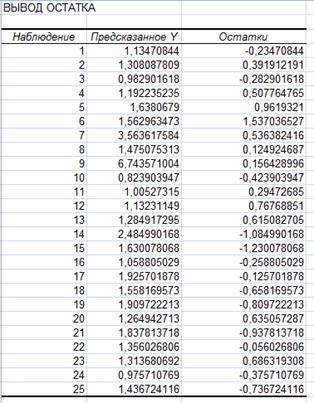
Y=0,148+0,008*x1+0,019*x2

r yx1	0,863
ryx2	0,005
rx1x2	0,395
r yx1x2	0,937
ryx2x1	-0,723
rx1x2y	0,772
R yx1x2	0,937
R^2 yx1x2	0,878
сигма ост	0,003
Fрасч	72,08
Fтабл	2,086
стьюдента	34,40

Линейный коэффициент корреляции может быть определен по формуле:

Или

.

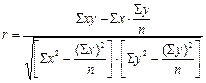Он изменяется в диапазоне от -1 до +1. положительный коэффициент характеризует прямую связь, отрицательный – обратную. Связь между факторным и результативным признаком можно признать тесной, если r>0,7.

Индекс корреляции может рассчитываться по формуле:

,

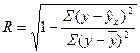Индекс корреляции изменяется от 0 до 1.

оценка существенности связи на основе t – критерия Стьюдента (при оценке параметров) или F – критерия Фишера (при оценке уравнения регрессии).

для линейной формы связи,

для криволинейной формы связи,

где k – число параметров.

Нахождение аппроксимирующего уравнения, для чего определяется средняя ошибка аппроксимации

.

F -критерия Фишера: