Лабораторная работа: Корреляционно-регрессионный анализ

Выполнила студентка гр.8431

Гарбузова Ю.

Егарева Т. Н

Ерошенко Н.Н

Проверила

Фетисова Г.В

Великий Новгород

2010

Корреляционный анализ изучает стохастические связи между случайными величинами в экономике. Метод корреляции применяется для того, чтобы при сложном взаимодействии посторонних влияний выявить зависимость между результатом и факторами в том случае, если посторонние факторы не изменялись и не искажали основную зависимость. При этом число наблюдений должно быть достаточно велико, так как малое число наблюдений не позволяет обнаружить закономерность связи. Укрупненно можно рекомендовать: число наблюдений равно восьмикратному числу факторов, включенных в модель.

Задание:

1.) Построить корреляционное поле зависимости между y и x1. Сделать вывод относительно формы и направления связи.

2.) Построить уравнение регрессии между у и х1 (линейная, степенная, логарифмическая). Оценить каждую функцию через F-критерий, , ошибку аппроксимации.

3.) Построить корреляционное поле зависимости между y и x2. Сделать вывод относительно формы и направления связи.

4.) Построить двухфакторное уравнение регрессии между y, x1,x2. Оценить показатели тесноты связи.

5.) Оценить модель через F-критерий Фишера.

6.) Оценить параметры через t-критерий Стьюдента.

Исходные данные :

Уравнение регрессии между у и х1 (линейная):

F расч = (0,7451/(1-0,7451))*((25-1-1)/1) = 67,232

Уравнение регрессии между у и х1 (логарифмическая):

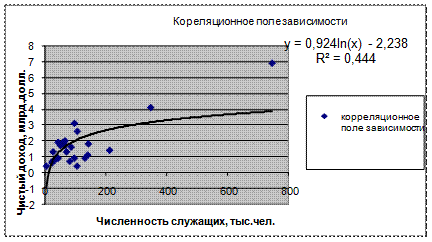
F расч = (0,4445/(1-0,4445))*((25-1-1)/1) = 18,404

Уравнение регрессии между у и х1 (степенная):

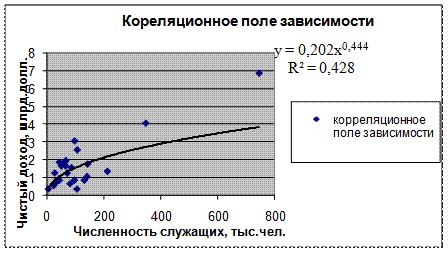
F расч = (0,4284/(1-0,4284))*((25-1-1)/1) = 0,019

линейная	F расч	67,23146332
логарифмическая	F расч	18,40414041
степенная	F расч	0,019459742

Е1	53,9
Е2	72,5
Е3	48,2

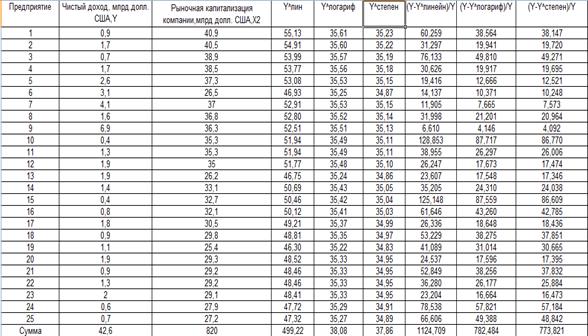
Уравнение регрессии между у и х2 (линейная):

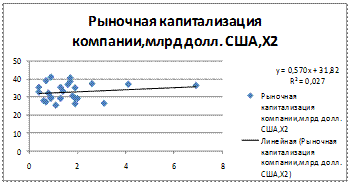
Уравнение регрессии между у и х2(логарифмическая):

--> ЧИТАТЬ ПОЛНОСТЬЮ <--