Лабораторная работа: Математическая статистика
8) Определяем границы доверительного интервала для математического ожидания по формулам
![]()
![]()
При заданной доверительной вероятности ![]() по таблицам распределения Стьюдента
по таблицам распределения Стьюдента ![]() , поэтому имеем
, поэтому имеем
![]()
![]()
9) Среднеквадратичное отклонение оценки математического ожидания случайной величины Х равно
![]()
![]()
10) По виду гистограммы выдвигаем гипотезу Н0 о подчинении случайной величины Х нормальному закону распределения. Для построения теоретической функции ![]() и
и ![]() составляем таблицу значений (таблица 3) нормальной величины
составляем таблицу значений (таблица 3) нормальной величины ![]() , определяем функцию Лапласа
, определяем функцию Лапласа ![]() , значения функции распределения на концах отрезков
, значения функции распределения на концах отрезков ![]() и вероятность попадания
и вероятность попадания![]() в i-тый интервал по формуле
в i-тый интервал по формуле ![]()
11) Рисунок 2 с эмпирической функцией распределения дополняем теоретической функцией F(x), значения которой найдены на концах интервалов.
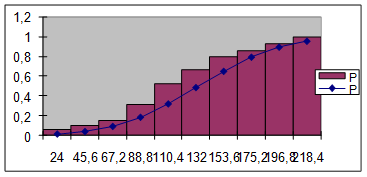
Рис. 3. Эмпирическая ![]() , теоретическая
, теоретическая ![]() функция распределения.
функция распределения.
12) Для проверки согласия выдвинутой гипотезы о о законе распределения экспериментальным данным находим вероятность ![]() попадания опытных данных в i-тый интервал от
попадания опытных данных в i-тый интервал от ![]() до
до![]() на основе полученных значений функции
на основе полученных значений функции ![]() на границах интервалов. На построенную раньше гистограмму наносим точки с координатами
на границах интервалов. На построенную раньше гистограмму наносим точки с координатами ![]() и соединяем их плавными линиями (Рис. 4). Сравнивая вид гистограммы и плотность
и соединяем их плавными линиями (Рис. 4). Сравнивая вид гистограммы и плотность ![]() распределения, необходимо убедиться в их адекватности, близости их характеров.
распределения, необходимо убедиться в их адекватности, близости их характеров.
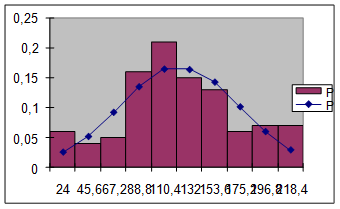
Рис. 4. Гистограмма относительных частот и теоретическая плотность вероятности ![]() .
.
13) При количественной оценке меры близости эмпирического и теоретического законов распределения можно использовать критерии Пирсона или Колмогорова.
а) по критерию Колмогорова:
Максимальное значение модуля разности между значениями эмпирической и теоретической функциями(см. рис. 3) наблюдается в точке, близкой к представителю ![]() . Тогда
. Тогда
![]()
Вычисляем величину
![]()
где r – объём выборки из представителей интервалов
![]() , следовательно
, следовательно ![]() . Так как
. Так как ![]() , поэтому гипотеза о нормальном распределении по критерию Колмогорова принимается как не противоречащая опытным данным.
, поэтому гипотеза о нормальном распределении по критерию Колмогорова принимается как не противоречащая опытным данным.
б) Для вычисления ![]() таблицу 3 дополняем промежуточными результатами
таблицу 3 дополняем промежуточными результатами ![]() ,
,![]() ,
, ![]() . Объединяем 1,2,3 и 9,10. Тогда
. Объединяем 1,2,3 и 9,10. Тогда ![]() . Получаем, что
. Получаем, что
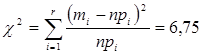
Для нормального закона распределения ![]() . Тогда число степеней свободы
. Тогда число степеней свободы ![]() . При
. При ![]() имеем
имеем ![]() . Поэтому гипотеза по критерию
. Поэтому гипотеза по критерию ![]() Пирсона принимается.
Пирсона принимается.
14) Составляем точечную диаграмму в декартовой (рис. 5) системе координат, где по оси абсцисс откладываем значение ![]() , а по оси ординат -
, а по оси ординат - ![]() . Пары значений
. Пары значений ![]() представляем на диаграмме в виде точек. На диаграмму наносим сетку равноотстоящих горизонтальных и вертикальных прямых. Расстояние между двумя вертикальными прямыми выражает длину
представляем на диаграмме в виде точек. На диаграмму наносим сетку равноотстоящих горизонтальных и вертикальных прямых. Расстояние между двумя вертикальными прямыми выражает длину ![]() интервала по оси абсцисс, а расстояние между горизонтальными прямыми – длину интервала
интервала по оси абсцисс, а расстояние между горизонтальными прямыми – длину интервала ![]() по оси ординат.
по оси ординат.
15) Для вычисления коэффициента корреляции составляется корреляционная таблица (таблица 4). В последние две строки заносятся промежуточные результаты для вычисления точечной оценки коэффициента корреляции
