Лабораторная работа: Математическая статистика
![]()
Вычисляем величину
![]()
где r – объём выборки из представителей интервалов
![]() , следовательно
, следовательно ![]() . Так как
. Так как ![]() , поэтому гипотеза о нормальном распределении по критерию Колмогорова принимается как не противоречащая опытным данным.
, поэтому гипотеза о нормальном распределении по критерию Колмогорова принимается как не противоречащая опытным данным.
б) Для вычисления ![]() таблицу 3 дополняем промежуточными результатами
таблицу 3 дополняем промежуточными результатами ![]() ,
,![]() ,
, ![]() . Объединяем 1,2,3 и 9,10. Тогда
. Объединяем 1,2,3 и 9,10. Тогда ![]() . Получаем, что
. Получаем, что
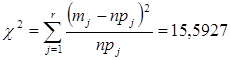
Для нормального закона распределения ![]() . Тогда число степеней свободы
. Тогда число степеней свободы ![]() . При
. При ![]() имеем
имеем ![]() . Поэтому гипотеза по критерию
. Поэтому гипотеза по критерию ![]() Пирсона принимается.
Пирсона принимается.
14) Составляем точечную диаграмму в декартовой системе координат, где по оси абсцисс откладываем значение ![]() , а по оси ординат -
, а по оси ординат - ![]() . Пары значений
. Пары значений ![]() представляем на диаграмме в виде точек. На диаграмму наносим сетку равноотстоящих горизонтальных и вертикальных прямых. Расстояние между двумя вертикальными прямыми выражает длину
представляем на диаграмме в виде точек. На диаграмму наносим сетку равноотстоящих горизонтальных и вертикальных прямых. Расстояние между двумя вертикальными прямыми выражает длину ![]() интервала по оси абсцисс, а расстояние между горизонтальными прямыми – длину интервала
интервала по оси абсцисс, а расстояние между горизонтальными прямыми – длину интервала ![]() по оси ординат.
по оси ординат.
15) Для вычисления коэффициента корреляции составляется корреляционная таблица (таблица 4). В последние две строки заносятся промежуточные результаты для вычисления точечной оценки коэффициента корреляции

16) Находим
![]()
![]()
![]()
![]()
Следовательно, линейные приближения к регрессиям имеют вид:
![]()
![]()
На рисунке 3 представлены точечная диаграмма и линии регрессии X на Y и Y на X. Расположение точек ![]() на диаграмме и небольшое значение коэффициента корреляции указывают на слабую коррелированность случайных величин X и Y между собой.
на диаграмме и небольшое значение коэффициента корреляции указывают на слабую коррелированность случайных величин X и Y между собой.
Таблица 2
| № интервала | ||||||||||
| 1 | 19 | 29,65 | 10 | 10 | 0,1 | 0,1 | 296,5 | -93,933 | 8823,408 | 88234,08 |
| 2 | 40,3 | 50,95 | 3 | 13 | 0,03 | 0,13 | 152,85 | -72,633 | 5275,553 | 15826,66 |
| 3 | 61,6 | 72,25 | 10 | 23 | 0,1 | 0,23 | 722,5 | -51,333 | 2635,077 | 26350,77 |
| 4 | 82,9 | 93,55 | 10 | 33 | 0,1 | 0,33 | 935,5 | -30,033 | 901,9811 | 9019,811 |
| 5 | 104,2 | 114,85 | 26 | 59 | 0,26 | 0,59 | 2986,1 | -8,733 | 76,26529 | 1982,898 |
| 6 | 125,5 | 136,15 | 10 | 69 | 0,1 | 0,69 | 1361,5 | 12,567 | 157,9295 | 1579,295 |
| 7 | 146,8 | 157,45 | 7 | 76 | 0,07 | 0,76 | 1102,15 | 33,867 | 1146,974 | 8028,816 |
| 8 | 168,1 | 178,75 | 10 | 86 | 0,1 | 0,86 | 1787,5 | 55,167 | 3043,398 | 30433,98 |
| 9 | 189,4 | 200,05 | 4 | 90 | 0,04 | 0,9 | 800,2 | 76,467 | 5847,202 | 23388,81 |
| 10 | 210,7 | 221,35 | 10 | 100 | 0,1 | 1 | 2213,5 | 97,767 | 9558,386 | 95583,86 |
| 11 | 232 | |||||||||
| Сумма | 100 | 1 | 12358,3 | 300429 |
Таблица 3
| № интервала |
| |||||||
| 1 | 19 | -1,89849 | -0,4713 | 0,0287 | 0,0368 | 3,68 | 8,4681 | 0,421508 |
| 2 | 40,3 | -1,51183 | -0,4345 | 0,0655 | 0,0659 | 6,59 | ||
| 3 | 61,6 | -1,12517 | -0,3686 | 0,1314 | 0,0982 | 9,82 | ||
| 4 | 82,9 | -0,73852 | -0,2704 | 0,2296 | 0,1336 | 13,36 | 11,2896 | 0,84503 |
| 5 | 104,2 | -0,35186 | -0,1368 | 0,3632 | 0,1488 | 14,88 | 123,6544 | 8,310108 |
| 6 | 125,5 | 0,034799 | 0,012 | 0,512 | 0,1508 | 15,08 | 25,8064 | 1,7113 |
| 7 | 146,8 | 0,421457 | 0,1628 | 0,6628 | 0,1282 | 12,82 | 33,8724 | 2,642153 |
| 8 | 168,1 | 0,808114 | 0,291 | 0,791 | 0,092 | 9,2 | 30,6916 | 1,6626 |
| 9 | 189,4 | 1,194772 | 0,383 | 0,883 | 0,0599 | 5,99 | ||
| 10 | 210,7 | 1,58143 | 0,4429 | 0,9429 | 0,0327 | 3,27 | ||
| 11 | 232 | 1,968087 | 0,4756 | 0,9756 | ||||
| Сумма | 13,5927 |