Лабораторная работа: Моделирование пассивных и активных фильтров
ЦЕЛЬ РАБОТЫ
Пользуясь программной средой Electronics Workbench смоделировать: пассивные фильтры низкой частоты (ФНЧ), однозвенные и двухзвенные; пассивные фильтры высокой частоты (ФВЧ), однозвенные и двухзвенные; полосовой и режекторный фильтры (ППФ); активный ФНЧ на ОУ; активный ФВЧ на ОУ; полосовой фильтр активного типа.
С помощью программы FilterLab построить АЧХ и ФЧХ, смоделировать электрические схемы для фильтров Баттерворта и Чебышева.
ХОД РАБОТЫ
1. Параметры элементов однозвенного пассивного ФНЧ рассчитываются, исходя из требуемой частоты среза f0 и принятого волнового сопротивления р. В рассматриваемом примере имеем при f0 = 10 000 Гц и ![]() = 8 Ом:
= 8 Ом:
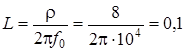 мкГн,
мкГн,
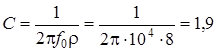 мкФ.
мкФ.
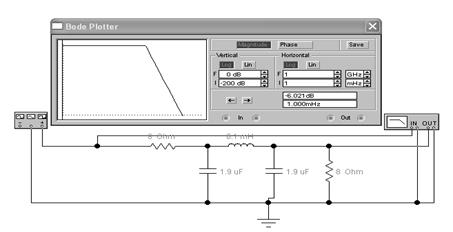
Рисунок 1 - Пассивный фильтр низкой частоты (ФНЧ), однозвенный.
В случае двухзвенного фильтра по сравнению с однозвенным, удается получить характеристику с более крутым фронтом.
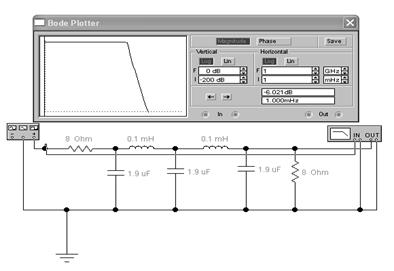
Рисунок 2 - Пассивный фильтр низкой частоты (ФНЧ), двухзвенный.
2. Параметры элементов однозвенного ФВЧ рассчитываются, исходя из требуемой частоты среза f0 и принятого волнового сопротивления р. В рассматриваемом примере имеем при f0 = 300 Гц и ![]() = 8 Ом:
= 8 Ом:
![]() мкГн,
мкГн,
![]() мкФ.
мкФ.
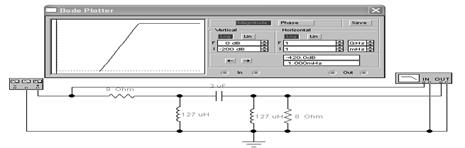
Рисунок 3 - Пассивный фильтр высокой частоты (ФВЧ), однозвенный.
В случае двухзвенного фильтра, по сравнению с однозвенным, удается получить характеристику с более крутым фронтом.
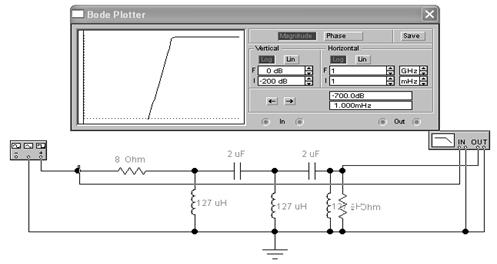
Рисунок 4 - Пассивный фильтр высокой частоты (ФВЧ), двухзвенный.
3. Параметры элементов двухконтурного полосового фильтра рассчитываются, исходя из центральной частоты фильтра f0 . При С = 1000*10-9 Ф и L = 0,25 мкГн имеем:
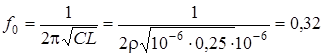 МГц.
МГц.
Далее резонансные частоты контуров раздвигаются, для чего емкость одного увеличивается на 1-2 %, другого - уменьшается. Чем шире должна быть получена полоса пропускания фильтра, тем больше это изменение емкости.
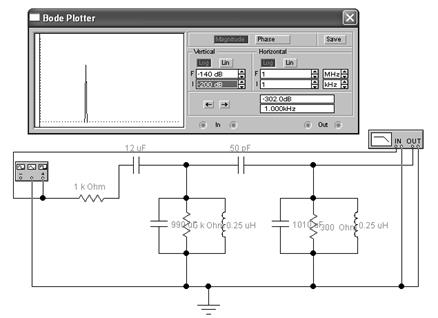
Рисунок 5 - Полосовой фильтр.
4. Параметры элементов трехконтурного режекторного фильтра, как и в предыдущем случае, рассчитываются исходя из центральной частоты фильтра f0 . В рассматриваемом случае центральная частота f0 = 0.32 МГц.
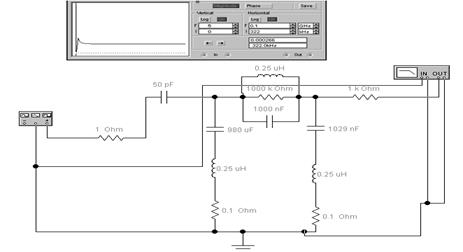
Рисунок 6 - Режекторный фильтр.
5. Комплексный коэффициент активного ФНЧ 1-го порядка определяется выражением:
--> ЧИТАТЬ ПОЛНОСТЬЮ <--