Лабораторная работа: Обеспечение надежности энергосистемы

,

где i – номер интервала; N – количество интервалов, соответствующих количеству разных ступеней графика нагрузок; - суммарная длительность нагрузки с уровнем за сутки.

Определение биноминальных коэффициентов и коэффициентов готовности групп однотипных генераторов.

Ряд распределения для i-й группы имеет вид многочлена

(6)

где ni – количество агрегатов в i -й группе;

mi – отключенные агрегаты в i -й группе;

(ni-mi) – находящиеся в работе агрегатыi -й группы;

Pгi – номинальная мощность агрегатов i -й группы;

– коэффициент (вероятность) работы генераторов i -й группы с мощностью .

Генерируемая мощность – случайная величина с биномиальной функцией распределения. Для расчета коэффициентов используем формулу биноминального распределения:

, (7)

где – биномиальный коэффициент;

– коэффициент вынужденного простоя mi генераторов (справочная величина);

– коэффициент готовности генераторов i-й группы.

Определим биноминальный коэффициентдля каждой группы генераторов по формуле:

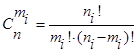, (8)

Далее по известным коэффициенту вынужденного простоя mi генераторов и коэффициенту готовности генераторов i-й группы в степени определим коэффициент готовности генераторов мощностью. Для этого воспользуемся формулой (6).

Генераторы 1ой группы
n	m1 откл ген	Генерация, кВт	n1 -m1	Cn1	Кг1-вероятность генерации
2	2	0	0	1	0,000064
2	1	30	1	2	0,015872
2	0	60	2	1	0,984064
Генераторы 2ой группы
n	m1 откл ген	Генерация, кВт	n1 -m1	Cn1	Кг1-вероятность генерации
3	3	0	0	1	0,000000512
3	2	25	1	3	0,000190464
3	1	50	2	3	0,023617536
3	0	75	3	1	0,976191488

Рн1		0	30	60
Кг1		0,000064	0,01587	0,984064
Рн	Кг
0	5,1E-07	3,2768E-11	8,13E-09	5,03841E-07
25	0,00019	1,21897E-08	3,02E-06	0,000187429
50	0,023618	1,51152E-06	0,000375	0,023241167
75	0,976191	6,24763E-05	0,015494	0,9606349

Таким образом мы определили вероятность совпадения вырабатываемой мощности обеими группами генераторов.

Третий блок – формирование вероятностной модели ЭЭС

Совпадение процессов производства и потребления во времени выразим через вероятностные модели этих процессов полученные в предыдущем блоке логической схемы.

Кн\Кг	0	25	30	50	55	60	75	80	85	105	110	135
27	-27	-2	3	23	28	33	48	53	58	78	83	108
40,5	-40,5	-15,5	-10,5	9,5	14,5	19,5	34,5	39,5	44,5	64,5	69,5	94,5
54	-54	-29	-24	-4	1	6	21	26	31	51	56	81
60,8	-60,8	-35,8	-30,8	-10,8	-5,75	-0,75	14,3	19,3	24,3	44,3	49,3	74,3
67,5	-67,5	-42,5	-37,5	-17,5	-12,5	-7,5	7,5	12,5	17,5	37,5	42,5	67,5
74,3	-74,3	-49,3	-44,3	-24,3	-19,3	-14,3	0,75	5,75	10,8	30,8	35,8	60,8
81	-81	-56	-51	-31	-26	-21	-6	-1	4	24	29	54
87,8	-87,8	-62,8	-57,8	-37,8	-32,8	-27,8	-12,8	-7,75	-2,75	17,3	22,3	47,3
94,5	-94,5	-69,5	-64,5	-44,5	-39,5	-34,5	-19,5	-14,5	-9,5	10,5	15,5	40,5
135	-135	-110	-105	-85	-80	-75	-60	-55	-50	-30	-25	0

Данная модель точно показывает при каких сочетаниях нагрузки и генерации возникает дефицит, а при каких профицит. Заметим что бездефицитное состояние показывает положительное значение. Такое представление модели приблизит ее к практически важной оценки недоотпуска электроэнергии вследствие возникновения дефицитных состояний.

Блоки: определение коэффициента бездефицитной работы и индекса надежности.

Коэффициент бездефицитной работы определяется по вероятностной модели функционирования ЭЭС полученной путем вычленения состояний энергосистемы, в которых дефицит не возникает, т.е. при , и суммирования вероятностей возникновения этих состояний:

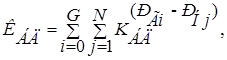
где - уровни располагаемой мощности энергосистемы, в составе которой G генераторов на интервале i = 0,G ; - ступени пронумерованной на интервале j = 1, N нагрузки в соответствие с графиком нагрузки.

Определение коэффициента готовности ЭС.

Коэффициент готовности определим по формуле:

К_г = ( Э – DЭ)/Э,